Counter-Based Pseudo-Random Number Generators on the GPU

Pseudo-random number generators (PRNGs) are essential for many types of computer programs (e.g. those such as path tracing, which employ Monte Carlo methods).

The Sequential Nature of Many PRNGs

However, most PRNGs rely on state to generate a number. Each time a number is generated, the state is updated. Logically, we can think of this process as a recurrence relation

\[s_{n+1} = u(s_n)\]

where \(s_n\) is the \(n\)-th state, \(u\) is a function which updates the state, and an initial state \(s_0\) is given. Then, a function \(r\) operates on the \(n\)-th state \(s_n\) to produce the \(n\)-th random number \(r_n\):

\[r_n = r(s_n).\]

Thus, the random numbers are computed as follows:

• \(r_0 = r(s_0), s_1 = u(s_0)\)
• \(r_1 = r(s_1), s_2 = u(s_1)\)
• \(r_2 = r(s_2), s_3 = u(s_2)\)
• \(r_3 = r(s_3), s_4 = u(s_3)\)
• ...

and so forth. Thus, using such a method, numbers can only be computed sequentially; to compute the \((n+1)\)-th state, the \(n\)-th state must be computed, and so on and so forth.

Parallel Algorithms and PRNGs

This is highly problematic when designing parallel algorithms which execute on multi-core CPUs or GPUs. One solution is to use multiple PRNGs, each with its own initial state. However, some PRNGs require a significant amount of storage for the state, and duplicating this state many times could require an unacceptable amount of overall storage. Furthermore, for some algorithms, it is important that each parallel process utilize the same PRNG sequence (for instance, if each process is supposed to draw a sample from a common distribution). Additionally, in some algorithms, it is necessary to recall random numbers generated previously, which necessitates storing the random numbers, which, again introduces substantial storage overhead.

Counter-Based RNGs

However, there is one good solution to all of these issues: counter-based pseudo-random number generators.

Counter-based pseudo-random number generators (CBRNGs) generate the \(n\)-th random number as a function of the index \(n\) itself (and typically some constant seed parameter). Thus, the \(n\)-th random number \(r_n\) is computed as

\[r_n = r(n, s),\]

where \(r(n, s)\) is a function of \(n\) and some constant seed parameter \(s\). CBRNGs require no storage beyond the constant seed parameter \(s\) (which is typically very small), they permit parallel processes to sample uniform random numbers from a single sequence (e.g. if each process requires \(m\) samples, then process \(n\) can obtain the \(k\)-th sample as \(r(n \cdot m + k, s)\)), and it is easy to recall a number generated at a prior sample (simply input the index of the prior sample).

The Squares CBRNG

An excellent example of a CBRNG is the Squares CBRNG, which is described in the paper Squares: A Fast Counter-Based RNG [1] and the earlier paper Middle-Square Weyl Sequence RNG [2] by author Bernard Widynski.

The author describes versions with 32-bit and 64-bit outputs, but we will only make use of the 32-bit version.

The example C source code from the most recent paper [1] is as follows:

inline static uint32_t squares32(uint64_t ctr, uint64_t key) {
  uint64_t x, y, z;
  y = x = ctr * key; z = y + key;
  x = x*x + y; x = (x>>32) | (x<<32); /* round 1 */
  x = x*x + z; x = (x>>32) | (x<<32); /* round 2 */
  x = x*x + y; x = (x>>32) | (x<<32); /* round 3 */
  return (x*x + z) >> 32; /* round 4 */
}

Weyl Sequences

The Squares CBRNG is based on a Weyl sequence, which alludes to the equidistribution theorem proved by Hermann Weyl which states that the sequence of multiples of an irrational number \(\alpha\) is equidistributed modulo 1. There is a corresponding version of this theorem for integer sequences: the sequence of integer multiples of an integer \(k\) is equidistributed modulo an integer \(m\) (if \(k\) is relatively prime to \(m\)). In other words, the sequence

\[0 ~\mathrm{mod}~ m, k ~\mathrm{mod}~ m, 2k ~\mathrm{mod}~ m, 3k ~\mathrm{mod}~ m, \dots\]

is uniformly distributed in the interval \([0, m)\), i.e. its probability mass function \(p(x)\) is constant (each remainder \(0 \dots m-1\) is equally likely to occur):

\[p(x) = \frac{1}{m}.\]

64-bit unsigned integer arithmetic is performed modulo \(m=2^{64}\). Thus \(k\) is chosen to be odd (since odd numbers are relatively prime to the even number \(2^{64}\)).

To see that the Weyl sequence is indeed uniformly distributed in the restricted case of a finite sequence of length \(2^{64}\), consider the following proof by contradiction (which follows Widynski's proof in this paper [2]). Consider an arbitrary element of a Weyl sequence \(w_i\) of length \(2^{64}\), where \(k\) is an odd number (it must be odd to be relatively prime with \(2^{64}\)):

\[w_i = i \cdot k ~\mathrm{mod}~2^{64}.\]

Suppose that \(w_{i_1} = w_{i_2}\) for \(0 \lt i_2 \lt i_1 \lt 2^{64}\). Then \(i_1 \cdot k ~\mathrm{mod}~2^{64} = i_2 \cdot k ~\mathrm{mod}~2^{64}\) (denote this common value as \(c\)). This, by definition, means that there exist integers \(q_1, q_2\) such that \((i_1 \cdot k) = c + q_1 \cdot 2^{64}\) and \((i_2 \cdot k) = c + q_2 \cdot 2^{64}\), and thus \((i_1 - i_2) \cdot k = (q_1 - q_2) \cdot 2^{64}\). Then \((i_1 - i_2) \cdot k = q \cdot 2^{64}\) where \(q = q_1 - q_2\).

Suppose that \(i_1 - i_2\) is odd. Then the product \((i_1 - i_2) \cdot k\) is likewise odd since \(k\) is odd, but \( q \cdot 2^{64}\) is even, which is a contradiction.

Thus, suppose that \(i_1 - i_2\) is even. Every even number can be factorized as \(2^j \cdot p\) for some odd integer \(p\). Then \(2^j \cdot p \cdot k = q \cdot 2^{64}\) and hence \(p \cdot k = q \cdot 2^{64 - j}\). Again, the left-hand side is odd and the right-hand side is even, which is a contradiction. Therefore, \(w_{i_1} \neq w_{i_2}\).

The Squares CBRNG uses a 64-bit unsigned integer counter (which represents the integer multiple \(0,1,2\dots\)) and a 64-bit unsigned integer key (which represents the constant \(k\)), with \(m=2^{64}\). This means that there are \(2^{64}\) elements in the sequence (one for each counter), although there are only \(2^{32}\) distinct values, since only the higher-order \(32\) bits are used for the output. Since the probability mass function for the 64-bit integers is

\[p(x) = \frac{1}{2^{64}},\]

and each 32-bit output occurs exactly \(2^{32}\) times (there are \(2^{32}\) 64-bit words with the same higher-order 32 bits), this means that the probability of any given output is

\[p_o(x) = 2^{32} \cdot p(x) = 2^{32} \cdot \frac{1}{2^{64}} = \frac{1}{2^{32}}.\]

Randomization with Uniformity

The Weyl sequence ensures uniformity, but it exhibits a clear pattern (it is not "random"). The Weyl sequence can be permuted to result in a "randomized" sequence.

Next, consider the following proof, adapted from Widynski's proof in this paper [2]. Consider a uniform, but not necessarily "random" finite sequence \((w_i)\) of length \(n\) with probability mass function \(p_w(w_i)\) and a "random", but not necessarily uniform finite sequence \((x_i)\) of length \(n\) with probability mass function \(p_x(x_i)\). Suppose that each element \(w_i\) of the former sequence is computed modulo \(n\) (and is hence less than \(n\)). In modular arithmetic (modulo \(n\)), given an integer \(y\) and an integer \(x\), there is a unique integer \(w(x,y)\) less than \(n\) such that \((x + w(x,y)) ~\mathrm{mod} ~n = y\). Next, consider the sequence \(((x_i + w_i)~\mathrm{mod} ~n)\) produced by summing these two sequences index-wise with addition modulo \(n\). The probability that a given integer \(y\) will appear in the resultant sequence is the probability that some \(x_i\) will appear at the same index as \(w(x_i,y)\). The probability of \(x_i\) coinciding with \(w(x_i, y)\) is given by the product \(p_x(x) \cdot p_w(w(x,y))\), and the probability that this will occur for some \(x_i\) is then given by the sum

\begin{align}p(y) &= \sum_{i=0}^{n-1}p_x(x_i) \cdot p_w(w(x_i, y)) \\&= \sum_{i=0}^{n-1}p_x(x_i) \cdot \frac{1}{n} \\&= \frac{1}{n}\cdot\sum_{i=0}^{n-1}p_x(x_i) \\&= \frac{1}{n} \cdot 1 \\&= \frac{1}{n}.\end{align}

Thus, the new sequence is likewise uniformly distributed. The idea, then, is to add the Weyl sequence to a sufficiently "random" sequence to produce a sequence that is both "random" and uniformly distributed.

Middle Square Method

The Squares CBRNG combines a Weyl sequence with a sequence produced by a modification of the middle square method described by John von Neumann. The idea is simple: square an \(n\)-digit number (represented in a suitable base), and take its middle \(n\) digits. For instance, in base 10 (decimal)

\[435698^2 = 189832747204,\]

and the middle \(6\) digits are \(832747\). The value \(n\) must be even, and zeroes are added as padding if \(2^n\) isn't at least \(2n\) digits in length, etc.

The Squares CBRNG implicitly works with 16-digit numbers in hexadecimal (base 16). Widynski offers the following example in this paper [2]: the square of the hexadecimal number E3296D171EC4A36F is

C9927E2B2075471D31C2914AAE4E8A21

This is a 128-bit (32 hexadecimal digit) result. Since the algorithm uses 64-bit integers, only the lower 64 bits (16 digits) are retained (modular arithmetic), namely 31C2914AAE4E8A21. The rotation operation (x >> 32 | x << 32) permutes this to AE4E8A2131C2914A. Then, the lower portion is returned, namely 31C2914A. Thus, the lower half of the middle of the square is returned.

One serious defect of the original middle square method is that it eventually produces repeating cycles of outputs, often even cycles of zeroes. However, Widynski offers a proof in this paper [2] that this cannot occur when the adapted squares method is added to a Weyl sequence.

Thus, the Squares CBRNG can be understood as combining a Weyl sequence based on a counter and key with a "random" sequence based on multiple rounds of an adapted version of the middle square method.

Computing Keys

The Squares CBRNG requires keys to be computed subject to certain constraints. First, the key must be odd (to be coprime with \(2^{64}\)). Second, there must be appropriate variation in the digits of the key to ensure sufficient randomness. Widynski suggests in [2] the following heuristic (in terms of hexadecimal representations of keys):

• The least significant digit should be odd
• No \(0\) digits will be used
• The upper 8 digits should be unique
• The lower 8 digits should be unique

For instance, the following keys satisfy these constraints:

• 0x97bec34dc1824d57
• 0x34a96b8edf456bc3
• 0x4a8579b1fe598b41
• 0xa95c36821e3b789d

These keys can be generated at runtime or pre-generated. Widynski has published key-generation code and pre-generated keys on a website.

Empirical Tests

The Squares CBRNG has been subjected to various statistical tests (BigCrush, PractRand) without failure.

WebGPU Implementation of Squares CBRNG

WebGPU, as the name implies, is indeed a standardized GPU interface in JavaScript which enables GPU applications to run inside a web browser. However, it is additionally a cross-platform, generic interface to GPU programming. Rather than develop multiple versions of an application (for Metal, Vulkan, DirectX, etc.), a single application can be developed in WebGPU. It can run outside the context of the browser as well, for instance, via the Rust implementation wgpu.

With WebGPU, programs dispatched on the GPU are written in a language called the WebGPU Shading Language (WGSL).

WGSL only supports 32-bit (and below) floating-point and integer types. However, both the 32-bit and 64-bit versions of the Squares CBRNG require 64-bit unsigned integer keys and counters.

One approach would be to implement a "Squares16" variant of the algorithm using u32 types, then to concatenate the results of two independent invocations together to form a 32-bit composite result. This would require twice as many operations.

However, in this post, we will investigate simulating 64-bit arithmetic via a custom U64 type. This will increase the number of operations significantly, but it will implement the algorithm in a direct manner, and will be amenable to "intrinsics" for hardware acceleration if WebGPU supports them (and there are proposals to do so).

Thus, we will define a 64-bit unsigned integer type as a struct U64 which is a pair of two u32 values representing the most significant bits hi and least significant bits lo.

struct U64 {
  hi: u32,
  lo: u32,
}

Addition

Two U64 values can be added component-wise, but we have to account for carrying. Since unsigned integers in WGSL use modular arithmetic, whenever a carry occurs, the result (i.e. the remainder) will be less than both of the addends. We could therefore compute the carry value as follows:

var carry: u32 = 0;
let lo_sum = a.lo + b.lo;
if lo_sum < a.lo {
  carry = 1;
}

However, this would result in thread divergence, since threads will execute different branches depending on the result of lo_sum < a.lo. Thus, we instead cast the boolean result to an unsigned integer u32(low_sum < lhs.low) and add the resulting integer (which will be 0 or 1). This results in the following implementation:

fn u64_add(a: U64, b: U64) -> U64 {
  let lo_sum = a.low + b.low;
  let carry = u32(lo_sum < a.low);
  return U64(a.high + b.high + carry, lo_sum);
}

Multiplication

Multiplication employs the familiar long multiplication algorithm. Consider Figure 1, which shows a specific example of 2-digit long multiplication using decimal numbers (note that multiplicative and additive "carries" have been deliberately separated in order to make the correspondence to the ensuing algorithm clearer).

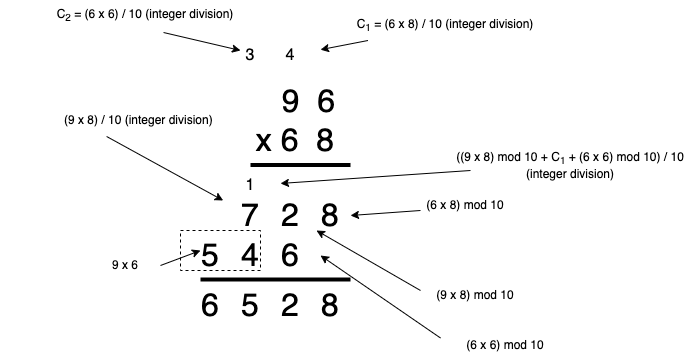
Next, consider this algorithm generalized to 2-digit multiplication in an arbitrary base, as in Figure 2.

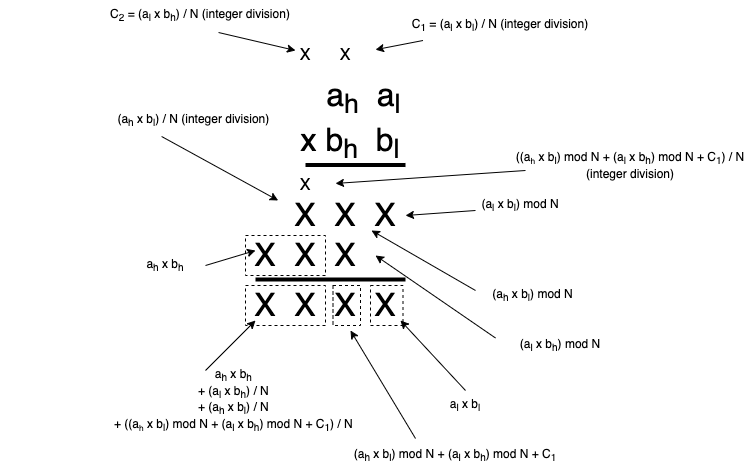
Multiplication of two 64-bit unsigned integers is performed modulo \(2^{64}\). This is conceptually equivalent to computing the 128-bit result and discarding the most significant 64 bits (i.e. retaining the least significant 64-bits). Thus, we are only interested in calculating the lower 64 bits of the result (the rightmost two digits in Figure 2). The number base of each digit is \(2^{32}\) (i.e. two 32-bit "digits" comprise the 64-bit word). Thus, as Figure 2 indicates, we want to compute the following:

• high: \(a_hb_l ~\mathrm{mod} 2^{32}~ + a_lb_h ~\mathrm{mod} 2^{32} + \lfloor a_lb_l / 2^{32} \rfloor\)
• low: \(a_lb_l\).

Note that, since arithmetic with u32 types is modular, this is equivalent to the following:

• high: ah * bh + al * bh + u32_mul_hi(al, bl)
• low: al * bl

fn u64_mul(a: U64, b: U64) -> U64 {
  let hi = u32_mul_hi(a.lo, b.lo);
  return U64(a.hi * b.lo + a.lo * b.hi + hi, a.lo * b.lo);
}

Now we need to describe the implementation of u32_mul_hi, which computes the most-significant 32 bits of the multiplication of two u32 values as a u32 value (i.e. the upper half of a 64-bit result). Thus, this is equivalent to integer division by \(2^{32}\) (i.e. \(\lfloor a_lb_l / 2^{32} \rfloor\)). This is accomplished via the long multiplication algorithm with the base set to \(2^{16}\), i.e. it performs 16-bit long multiplication. The product of two 16-bit integers fits inside a 32-bit integer, so the higher-order digit is collected as a u32. Note the following equivalences:

• \(x ~\mathrm{mod} 2^{16}\) = x & 0xffff (i.e. the modulus is the lower 16 bits)
• \(\lfloor x / 2^{16} \rfloor\) = x >> 16 (i.e. integer division selects the upper 16 bits)

The implementation then corresponds directly to long multiplication as depicted in Figure 2, yet with base 16.

fn u32_mul_hi(a: u32, b: u32) -> u32 {
  let ah = a >> 16;
  let bh = b >> 16;
  let al = a & 0xffff;
  let bl = b & 0xffff;
  let albl = al * bl;
  let ahbl = ah * bl;
  let albh = al * bh;
  let sum = (ahbl & 0xffff) + (albh & 0xffff) + (albl >> 16);
  return ah * bh + (ahbl >> 16) + (albh >> 16) + (sum >> 16);
}

WGSL may eventually support extended integer arithmetic operations (such as one equivalent to u32_mul_hi, which would be more efficient; there is a proposal to add them eventually.

Floating Point Output

It is typically most convenient for PRNGs to generate floating-point numbers in the range \([0, 1)\). To convert the u32 generated by the Squares32 CBRNG to an f32, rather than divide by \(2^{32}\) (which would require an f64 to accommodate the result), we perform a bitcast (i.e. we treat the bit representation of the u32 as the bit representation of an f32, which uses the IEEE floating point representation). Since we are only interested in the lower order 23 bits (which represent the mantissa) and the higher-order 9 bits represent the sign bit and the exponent, we mask with a bitwise "and" using the mask 0x7FFFFF, and then add the exponent bias of 127 (which represents an exponent of \(0\)) in the appropriate place (which is equivalent to the bitwise "or" with the constant 0x3f800000 = 127 << 23). Since the exponent represents a power of 2, and the significand is of the form \(1.m\) for the mantissa \(m\) in the range \([0, 1)\), the value is \(1.m \cdot 2^0 = 1.m\) and hence this will generate values in the range \([1,2)\), so we subtract \(1\) to yield the range \([0,1)\). Note that this means that we only generate \(2^{23}\) unique values (we are effectively computing modulo \(2^{23}\)), but the sequence length is still length \(2^{64}\), where each value will occur \(2^{41}\) times with probability \(1/2^{23}\). Some authors will instead use a right shift by 9, i.e. u >> 9. This will produce a different sequence of values but with an equivalent distribution of values, since u >> 9 is equivalent to \(\lfloor u/2^9 \rfloor\) and u & 0x7FFFFF is equivalent to \(u ~\mathrm{mod} ~2^{23}\), and, if the values are uniformly distributed, the divisions and remainders will be equally distributed, that is, the following sequences have the same distribution:

• \(\lfloor 0/2^9 \rfloor, \lfloor 1/2^9 \rfloor, \dots, \lfloor (2^{32}-1)/2^9 \rfloor\),
• \(0 ~\mathrm{mod} ~2^{23}, 1 ~\mathrm{mod} ~2^{23}, \dots, (2^{32}-1) ~\mathrm{mod} ~2^{23}\).

As a simple example, consider the sequence \(0 \dots 999\); produce a second sequence by dividing each number by \(10\) and a third sequence by computing the remainder when dividing by \(100\). Then, each sequence will have the same distribution of results (each number \(0 \dots 99\) will occur exactly \(10\) times).

Thus, we may write

fn rng_bitcast(u: u32) -> f32 {
  return bitcast<f32>((u & 0x7FFFFF) | (127 << 23)) - 1.0;
}

or

fn rng_bitcast(u: u32) -> f32 {
  return bitcast<f32>((u >> 9) | (127 << 23)) - 1.0;
}

Rotation

Finally, to implement the "rotation" (circular shift) operation which exchanges the higher and lower order words of a 64-bit integer (implemented as x >> 32 | x << 32 in the C example), we implement a simple swapping routine.

fn u64_swp(a: U64) -> U64 {
  return U64(a.lo, a.hi);
}

WGSL Implementation

Thus, the full implementation is as follows:

struct U64 {
  hi: u32,
  lo: u32,
}

fn rng(ctr: U64, key: U64) -> f32 {
  var x = u64_mul(ctr, key);
  var y = x;
  var z = u64_add(y, key);
  
  x = rng_round(x, y);
  x = rng_round(x, z);
  x = rng_round(x, y);
  x = u64_add(u64_sqr(x), z);
  
  return rng_bitcast(x.hi);
}

fn rng_bitcast(u: u32) -> f32 {
  return bitcast<f32>((u & 0x7FFFFF) | (127 << 23)) - 1.0;
}

fn rng_round(a: U64, b: U64) -> U64 {
  return u64_swp(u64_add(u64_sqr(a), b));
}

fn u64_add(a: U64, b: U64) -> U64 {
  let lo_sum = a.lo + b.lo;
  let carry = u32(lo_sum < a.lo); 
  return U64(a.hi + b.hi + carry, lo_sum);
}

fn u64_mul(a: U64, b: U64) -> U64 {
  let hi = u32_mul_hi(a.lo, b.lo);
  return U64(a.hi * b.lo + a.lo * b.hi + hi, a.lo * b.lo);
}

fn u64_sqr(a: U64) -> U64 { 
  let hi = u32_mul_hi(a.lo, a.lo); 
  return U64(2 * a.hi * a.lo + hi, a.lo * a.lo);
}

fn u64_swp(a: U64) -> U64 {
  return U64(a.lo, a.hi);
}

fn u64_copy(a: U64) -> U64 {
  return U64(a.hi, a.lo);
}

fn u32_mul_hi(a: u32, b: u32) -> u32 {
  let ah = a >> 16;
  let bh = b >> 16;
  let al = a & 0xffff;
  let bl = b & 0xffff;
  let albl = al * bl;
  let ahbl = ah * bl;
  let albh = al * bh;
  let sum = (ahbl & 0xffff) + (albh & 0xffff) + (albl >> 16);
  return ah * bh + (ahbl >> 16) + (albh >> 16) + (sum >> 16);
}

References

• [1] Squares: A Fast Counter-Based RNG by Bernard Widynski. Bernard Widynski. “Squares: A Fast Counter-Based RNG”. In: arXiv:2004.06278 (2020). url: https://arxiv.org/abs/2004.06278
• [2] Middle-Square Weyl Sequence RNG by Bernard Widynski. Bernard Widynski. “Middle-Square Weyl Sequence RNG”. In: arXiv:1704.00358 (2017). url: http://arxiv.org/abs/1704.00358

Further Reading

See also one of the original papers on CBRNGs: Parallel Random Numbers: As Easy as 1, 2, 3