Covariant Derivatives

This post discusses the concept of a covariant derivative on a smooth manifold, which is analogous to a directional derivative of a vector field.

Introduction

Much of differential geometry is about the generalization of concepts from "flat" Euclidean space to general, possibly "curved", smooth manifolds. In particular, we seek a generalization of the notion of a "straight line" or "shortest path". Intuitively, this should be a curve along the manifold whose acceleration is zero. Likewise, we also seek a way to "connect" the disparate tangent spaces along the manifold by "transporting" tangent vectors from one space to another along curves in a "parallel" manner. Each of these notions can be defined in an intrinsic manner with the aid of an appropriate notion of a directional derivative of a vector field.

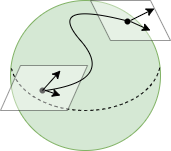
Directional Derivatives

Recall the definition of the directional derivative of a map \(f : X \rightarrow Y\) between normed vector spaces \(X\) and \(Y\) (in this post all vector spaces are real vector spaces):

Definition (Directional Derivative). The directional differential of a map \(f : V \rightarrow W\) between normed vector spaces \(V\) and \(W\) along the vector \(v \in V\) at the point \(p \in V\) is the vector in \(W\) denoted \(\nabla_vf(p)\) and defined to be the following limit:

\[\nabla_vf(p) = \lim_{t \to 0}\frac{f(p + t \cdot v) - f(p)}{t}.\]

If this limit exists for every \(v \in V\) and the map

\[\nabla_{(-)}f(p) = v \mapsto \nabla_vf(p)\]

is a bounded linear map, then the map \(\nabla_{(-)}f(p) : V \rightarrow W\) is called the directional derivative of \(f\) at \(p\).

Recall that the partial derivative is a directional derivative in the direction of a basis vector.

Definition (Partial Derivative). The partial derivative of a map \(f : V \rightarrow W\) between a finite-dimensional real normed vector space \(V\) of dimension \(n\) and a normed vector space \(W\) at the point \(p \in V\) is the vector in \(W\) denoted \((\partial f/\partial x^i)(p)\) and defined as

\[\frac{\partial f}{\partial x^i}(p) = \nabla_{e_i}f(p) = \lim_{t \to 0}\frac{f(p + t \cdot e_i) - f(p)}{t},\]

where \((e_i)\) is a given basis for \(V\) and \((x^i)\) are the coordinate functions with respect to this basis, i.e. \(v = x^i(v) \cdot e_i\) for every vector \(v \in V\).

In the case of a map \(f : \mathbb{R} \rightarrow W\), the standard basis for \(\mathbb{R}\) consists of a single basis vector \(e_1 = 1\) corresponding to the single component function \(x = \mathrm{Id}\), and the following notation is used:

\[\frac{df}{dx}(p) = \frac{\partial f}{\partial x}(p).\]

The directional derivative can then be defined as follows:

\[\nabla_vf(p) = \frac{d}{dt}\bigg\rvert_0f(p + t \cdot v).\]

Writing \(g(t) = f(p + tv)\) and expanding the definition, we obtain the original definition:

\[\frac{dg}{dt}(0) = \lim_{t \to 0}\frac{g(0 + t \cdot 1) - g(0)}{t} = \lim_{t \to 0}\frac{f(p + t \cdot v) - f(p)}{t}.\]

Also recall that limits in finite-dimensional normed vector spaces can be computed component-wise, which means that

\[\lim_{h \to a}f(h) = \left(\lim_{h \to a}f^j(h)\right) \cdot e_j,\]

where \((e_j)\) is a basis for \(W\), \(f : V \rightarrow W\) is a function, \(f^j : V \rightarrow \mathbb{R}\) are the component functions defined such that \(f(p) = f^j(p) \cdot e_j\), and \(a \in V\). In this case, it follows that

\[\nabla_vf(p) = \nabla_vf^j(p) \cdot e_j.\]

Thus, for a map \(f : V \rightarrow W\) between finite-dimensional normed vector spaces \(V\) and \(W\) with bases \((e_i)\) and \((e_j)\), respectively, it follows that

\begin{align}\nabla_vf(p) &= \nabla_vf^j(p) \cdot e_j \\&= \nabla_{v^i \cdot e_i}f^j(p) \cdot e_j \\&= v^i \cdot \nabla_{e_i}f^j(p) \cdot e_j \\&= v^i \cdot \frac{\partial f^j}{\partial x^i}(p) \cdot e_j.\end{align}

This implies that the map \(f\) can be represented in coordinates by its Jacobian matrix, defined as the \(m \times n\) matrix

\[\begin{bmatrix}\frac{\partial f^1}{\partial x^1}(p) & \dots & \frac{\partial f^1}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial f^m}{\partial x^1}(p) & \dots & \frac{\partial f^m}{\partial x^n}(p)\end{bmatrix}\]

since

\[\begin{bmatrix}\frac{\partial f^1}{\partial x^1}(p) & \dots & \frac{\partial f^1}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial f^m}{\partial x^1}(p) & \dots & \frac{\partial f^m}{\partial x^n}(p)\end{bmatrix}\begin{bmatrix}v^1 \\ \vdots \\ v^n\end{bmatrix} = \left(v^i \cdot \frac{\partial f^1}{\partial x^i}(p)\right) \cdot \begin{bmatrix}1 \\ \vdots \\ 0\end{bmatrix} + \dots + \left(v^i \cdot \frac{\partial f^m}{\partial x^i}(p)\right) \cdot \begin{bmatrix}0 \\ \vdots \\ 1\end{bmatrix}.\]

The directional derivative satisfies certain additional properties:

• Linearity (in \(f\)): \(\nabla_v(af)(p) = a \cdot \nabla_vf(p)\), and \(\nabla_v(f+g)(p) = \nabla_vf(p) + \nabla_vg(p)\),
• Product Rule: \(\nabla_v(fg)(p) = f(p) \cdot \nabla_vg(p) + g(p) \cdot \nabla_vf(p)\).

These requirements state that the map \(\nabla_v(-)(p) : C^{\infty}(V) \rightarrow \mathbb{R}\) is a derivation at a point.

Recall also that the directional derivative satisfies a chain rule:

\[\nabla_v(f \circ g)(p) = \nabla_{\nabla_vg(p)}f(g(p)).\]

We can then compute

\begin{align}\nabla_v(f \circ g)(p) &= \nabla_{\nabla_vg(p)}f(g(p)) \\&= \left[\nabla_vg(p)\right]_i \cdot \frac{\partial f}{\partial y^j}(g(p)) \cdot e_j \\&= v^i \cdot \frac{\partial g^j}{\partial x^i}(p) \cdot \frac{\partial f^i}{\partial y^j}(g(p)) \cdot e_j.\end{align}

This then implies that the derivative can be represented in coordinates as the product of the respective Jacobian matrices:

\[\begin{bmatrix}\frac{\partial f^1}{\partial y^1}(g(p)) & \dots & \frac{\partial f^1}{\partial y^p}(g(p)) \\ \vdots & \ddots & \vdots \\ \frac{\partial f^n}{\partial x^1}(g(p)) & \dots & \frac{\partial f^n}{\partial x^p}(g(p))\end{bmatrix} \begin{bmatrix}\frac{\partial g^1}{\partial x^1}(p) & \dots & \frac{\partial g^1}{\partial x^m}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial g^n}{\partial x^1}(p) & \dots & \frac{\partial g^m}{\partial x^n}(p)\end{bmatrix}.\]

Directional Derivatives of Vector Fields on \(\mathbb{R}^n\)

Next, consider the case of a smooth vector field on Euclidean space \(\mathbb{R}^n\), which is simply a smooth function \(f : \mathbb{R}^n \rightarrow \mathbb{R}^n\). Our goal is to extend the definition of the directional derivative of a function along a vector to the definition of a directional derivative of a vector field along another vector field.

Definition (Directional Derivative of Vector Fields on \(\mathbb{R}^n\)). The directional derivative of a smooth vector field \(X : \mathbb{R}^n \rightarrow \mathbb{R}^n\) along a smooth vector field \(Y : \mathbb{R}^n \rightarrow \mathbb{R}^n\) at the point \(p \in \mathbb{R}^n\) is the smooth vector field denoted \(\nabla_XY : \mathbb{R}^n \rightarrow \mathbb{R}^n\) and defined for each point \(p \in \mathbb{R}^n\) as

\[(\nabla_XY)(p) = \lim_{t \to 0}\frac{Y(p + t \cdot X(p)) - Y(p)}{t}.\]

This can alternatively be defined as follows:

\[(\nabla_XY)(p) = \frac{d}{dt}\bigg\rvert_0Y(p + t \cdot X(p)).\]

We want to verify that this notion of directional derivative satisfies the same properties as the usual notion of directional derivative.

First, let's verify that \(\nabla_XY\) is "linear" in \(X\). To make this precise, first note that smooth functions \(f \in C^{\infty}(\mathbb{R}^n)\) form a ring and that smooth vector fields \(\mathfrak{X}(\mathbb{R}^n)\) form a module over \(C^{\infty}(\mathbb{R}^n)\). A module is analogous to a vector space, and a ring is analogous to the respective scalar field of the vector space. Thus, the analogous requirement is that the map \(\nabla_{(-)}Y\) should be a module homomorphism, which is analogous to a linear map. Thus, we require the following:

• \(\nabla_{fX}Y = f \cdot \nabla_XY\) for all \(f \in C^{\infty}(\mathbb{R}^n)\),
• \(\nabla_{X_1 + X_2}Y = \nabla_{X_1}Y + \nabla_{X_2}Y\) for all \(X_1,X_2 \in \mathfrak{X}(\mathbb{R}^n)\).

A smooth vector field \(X : \mathbb{R}^n \rightarrow \mathbb{R}^n\) can be expressed in terms of the standard basis \((e_i)\) on \(\mathbb{R}^n\) as

\[X(p) = X^i(p) \cdot e_i,\]

where \((X^i)\) are the component functions of \(X\).

Recall that Euclidean space is isomorphic to each of its tangent spaces, i.e. \(T_p\mathbb{R}^n \cong \mathbb{R}^n\), and thus this expression can be re-expressed in terms of the basis vectors \((\partial/\partial x^i)\rvert_p\) in \(T_p\mathbb{R}^n\) as follows:

\[X(p) = X^i(p) \cdot \frac{\partial}{\partial x^i}\bigg\rvert_p.\]

Writing this in "point-free" form as a vector field, we obtain

\[X = X^i \cdot \frac{\partial}{\partial x^i}.\]

Using the chain rule, we can compute an expression for \(\nabla_XY\) in coordinates:

\begin{align}(\nabla_XY)(p) &= \frac{d}{dt}\bigg\rvert_0Y(p + t \cdot X(p)) \\&= X^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) \cdot e_j.\end{align}

Recall that vector fields can be considered as derivations, and that the notation \(X(Y^j)\) denotes the following function (where \(X_p\) is a tangent vector at point \(p\)):

\[X(Y^j)(p) = X_p(Y^j) = X^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p).\]

Thus, \(\nabla_XY\) can be expressed as

\[(\nabla_XY)(p) = X(Y^j)(p) \cdot e_j,\]

or, in terms of the tangent space, as

\[(\nabla_XY)(p) = X(Y^j)(p) \cdot \frac{\partial}{\partial x^j}\bigg\rvert_p,\]

or in "point-free" form as a vector field as

\[\nabla_XY = X(Y^j) \cdot \frac{\partial}{\partial x^j}.\]

Then, again, using the chain rule, we compute

\begin{align}(\nabla_{fX}Y)(p) &= \frac{d}{dt}\bigg\rvert_0Y(p + t \cdot (fX)(p)) \\&= \frac{d}{dt}\bigg\rvert_0Y(p + t \cdot f(p) \cdot X(p)) \\&= f(p) \cdot X^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) \cdot e_j \\&= f(p) \cdot \nabla_XY(p).\end{align}

Similarly, using the chain rule, we compute

\begin{align}(\nabla_{X_1 + X_2}Y)(p) &= \frac{d}{dt}\bigg\rvert_0Y(p + t \cdot (X_1 + X_2)(p)) \\&= f(p) \cdot (X_1 + X_2)^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) \cdot e_j \\&= \left(X_1^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) \cdot e_j\right) + \left(X_2^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) \cdot e_j\right) \\&= \nabla_{X_1}Y(p) + \nabla_{X_2}Y(p).\end{align}

Thus, \(\nabla_XY\) is indeed "linear" in \(X\).

Next, we want to confirm that \(\nabla_XY\) is linear in \(Y\). The set of smooth vector fields \(\mathfrak{X}(\mathbb{R}^n)\) is a vector space under point-wise addition and point-wise scalar multiplication. Linearity follows directly from the properties of limits in normed vector spaces:

\begin{align}\nabla_X(aY)(p) &= \frac{d}{dt}\bigg\rvert_0(aY)(p+t\cdot X(p)) \\&= \frac{d}{dt}\bigg\rvert_0 a \cdot \left[Y(p+t\cdot X(p))\right] \\&= a \cdot \left[\frac{d}{dt}\bigg\rvert_0 Y(p+t\cdot X(p))\right] \\&= a \cdot \nabla_XY(p).\end{align}

\begin{align}\nabla_X(Y_1 + Y_2)(p) &= \frac{d}{dt}\bigg\rvert_0(Y_1 + Y_2)(p+t\cdot X(p)) \\&= \frac{d}{dt}\bigg\rvert_0 \left[Y_1(p+t\cdot X(p)) + Y_2(p+t\cdot X(p))\right] \\&= \frac{d}{dt}\bigg\rvert_0 \left[Y_1(p+t\cdot X(p))\right] + \frac{d}{dt}\bigg\rvert_0 \left[ Y_2(p+t\cdot X(p))\right] \\&= \nabla_XY_1(p) + \nabla_XY_2(p).\end{align}

Finally, we want to confirm that \(\nabla_XY\) obeys some analog of the product rule. Since limits in finite-dimensional normed vector spaces are computed component-wise, it follows from the product rule for (ordinary) directional derivatives that

\begin{align}\frac{d}{dt}\bigg\rvert_0(fY)(p + t \cdot X(p)) &= \frac{d}{dt}\bigg\rvert_0\left(f(p + t \cdot X(p)) \cdot Y(p + t \cdot X(p))\right) \\&= \left[\frac{d}{dt}\bigg\rvert_0 \left(f(p + t \cdot X(p)) \cdot Y^j(p + t \cdot X(p))\right)\right] \cdot e_j \\&= \left[\left(f(p) \cdot \frac{d}{dt}\bigg\rvert_0Y^j(p + t \cdot X(p))\right) + \left(Y^j(p) \cdot \frac{d}{dt}\bigg\rvert_0 f(p + t \cdot X(p))\right) \right] \cdot e_j \\&= \left[f(p) \cdot \frac{d}{dt}\bigg\rvert_0Y^j(p + t \cdot X(p)) \right] \cdot e_j + \left[Y^j(p) \cdot \frac{d}{dt}\bigg\rvert_0 f(p + t \cdot X(p)) \right] \cdot e_j \\&= f(p) \cdot \left[\left(\frac{d}{dt}\bigg\rvert_0Y^j(p + t \cdot X(p))\right) \cdot e_j \right] + \left[\frac{d}{dt}\bigg\rvert_0 f(p + t \cdot X(p))\right] \cdot \left[Y^j(p) \cdot e_j\right] \\&= f(p) \cdot (\nabla_XY)(p) + (\nabla_Xf)(p) \cdot Y(p).\end{align}

Here, the notation \((\nabla_Xf)(p)\) refers to the directional derivative of the smooth function \(f\) in the direction of the vector field \(X\), i.e.

\[(\nabla_Xf)(p) = \frac{d}{dt}\bigg\rvert_0 f(p + t \cdot X(p)).\]

Directional Derivatives of Vector Fields on Smooth Manifolds

Our next goal is to extend the definition of the directional derivative of smooth vector fields in \(\mathbb{R}^n\) to smooth manifolds.

Consider the definition in \(\mathbb{R}^n\):

\[(\nabla_XY)(p) = \lim_{t \to 0}\frac{Y(p + t \cdot X(p)) - Y(p)}{t}.\]

If we attempt to apply this definition in an arbitrary smooth manifold, two immediate problems arise:

1. The addition \(p + t \cdot X(p)\) is undefined since \(p \in M\) is a point on a manifold, and \(X(p)\) is a tangent vector, and no such addition operation is available on a general manifold.
2. The subtraction \(Y(p + t \cdot X(p)) - Y(p)\) is undefined, since \(Y(p + t \cdot X(p))\) and \(Y(p)\) are tangent vectors in different tangent spaces, and no such addition operation is available on a general manifold.

Both of these problems can be solved by Lie derivatives. Here we will only briefly comment on Lie derivatives. The Lie derivative \(\mathcal{L}_XY\) solves the first problem by using the flow \(\theta\) of \(X\): essentially, the curve \(p + t \cdot X(p)\) is replaced with an integral curve, i.e. a differentiable curve \(\gamma : J \rightarrow M\) such that \(\gamma'(t) = Y_{\gamma(t)}\) for all \(t \in J\) for some interval \(J\), i.e. the "velocity" of the curve at each \(t\) matches the vector field's value at the point \(\gamma(t)\). The curve and the vector then become arbitrarily close in a sufficiently small neighborhood of each point. Lie derivatives solve the second problem by using the pushforward \(d\left(\theta_{-t}\right)_{\theta_t(p)}\) of a map \(\theta_{-t} : M \rightarrow M\) induced by the flow of \(X\), which "pushes" the tangent vector in \(T_{\theta_t(p)}M\) "forward" to a tangent vector in \(T_pM\) and thus ensures that the vectors being subtracted both belong to the same tangent space.

\[(\mathcal{L}_XY)_p = \lim_{t \to 0}\frac{d\left(\theta_{-t}\right)_{\theta_t(p)}\left(Y_{\theta_t(p)}\right) - Y_p}{t}.\]

However, although the Lie derivative is an important and useful generalization of a directional derivative, it is non-linear in each of its arguments, and so it differs from the usual notion of a derivative as a "best linear approximation", and it differs from the notion of derivative that we are presently considering (although the two notions are related).

The solution, then, is simply to define a notion of derivative using the desired properties as axioms. Such a derivative must be given along with a manifold; it is auxiliary structure which must be specified. This notion of directional derivative, for historical reasons, commonly goes by the name covariant derivative.

Definition (Affine Connection). An affine connection (also called a linear connection or just a connection on \(M\)) is a map

\[\nabla : \Gamma(TM) \times \Gamma(TM) \rightarrow \Gamma(TM)\]

written

\[(X,Y) \mapsto \nabla_XY\]

for all \(X,Y \in \Gamma(TM)\), where \(M\) is a smooth manifold, \(TM\) is the tangent bundle on \(M\), and \(\Gamma(TM)\) is the set of all smooth vector fields on \(TM\), such that the following properties are satisfied:

• \(\nabla_XY\) is linear over \(C^{\infty}(M)\) in \(X\) for all \(Y \in \Gamma(TM)\), i.e.
  • \(\nabla_{fX}Y = f \cdot \nabla_XY\) for all \(f \in C^{\infty}(M)\) and \(X \in \Gamma(TM)\) and
  • \(\nabla_{X_1+X_2}Y = \nabla_{X_1}Y + \nabla_{X_2}Y\) for all \(X_1,X_2 \in \Gamma(TM)\),
• \(\nabla_XY\) is linear over \(\mathbb{R}\) in \(Y\) for all \(X \in \Gamma(TM)\), i.e.
  • \(\nabla_X(a \cdot Y) = a \cdot \nabla_XY\) for all \(a \in \mathbb{R}\) and \(Y \in \Gamma(TM)\), and
  • \(\nabla_X(Y_1+Y_2) = \nabla_XY_1 + \nabla_XY_2\) for all \(Y_1,Y_2 \in \Gamma(TM)\),
• \(\nabla\) satisfies the following product rule for all \(X,Y \in \Gamma(TM)\) and \(f \in C^{\infty}(M)\):

\[\nabla_X(fY) = f \cdot \nabla_XY + \nabla_Xf \cdot Y,\]

where the notation \(\nabla_Xf\) indicates the directional derivative of \(f\) along \(X\) and is defined as

\[\nabla_Xf = Xf,\]

i.e. treating the smooth vector field \(X\) as a derivation on \(C^{\infty}(M)\), \(Xf : C^{\infty}(M) \rightarrow C^{\infty}(M)\) is the map

\[(Xf)(p) = X_pf.\]

Definition (Covariant Derivative). Given an affine connection \(\nabla\) on a smooth manifold \(M\), the covariant derivative of a smooth vector field \(Y \in \Gamma(TM)\) along a smooth vector field \(X \in \Gamma(TM)\) is the smooth vector field \(\nabla_XY\).

The Connection in Coordinates

Next, we will consider what an affine connection looks like in coordinates relative to an arbitrary frame \((E^j)\). We compute as follows:

\begin{align}\nabla_XY &= \nabla_X(Y^j E_j) \\&= X(Y^j)E_j + Y^j\nabla_XE_j & \text{(product rule)}\\&= X(Y^j)E_j + Y^j\nabla_{X^iE_i}E_j \\&= X(Y^j)E_j + X^iY^j\nabla_{E_i}E_j & \text{(linearity)}.\end{align}

Thus, the connection can be fully analyzed in terms of its action on pairs of vector fields from the respective frame:

\[\nabla_{E_i}E_j.\]

Since \(\nabla_{E_i}E_j\) is a vector field, it can be expressed as a linear combination of the same frame:

\[\nabla_{E_i}E_j = \Gamma^k_{ij}E_k,\]

where, for each \(i\) and \(j\), the connection coefficient \(\Gamma^k_{ij}\) denotes the \(k\)-th coordinate function of \(\nabla_{E_i}E_j\) relative to the frame. If the manifold has dimension \(n\), this implies that there are \(n^3\) coordinate functions, one for each index \(i\), \(j\), and \(k\). Thus, we may write

\[\nabla_XY = X(Y^j)E_j + X^iY^j\Gamma^k_{ij}E_k.\]

Renaming the dummy index \(j\) to \(k\), we obtain

\[\nabla_XY = \left(X(Y^k) + X^iY^j\Gamma^k_{ij}\right)E_k.\]

In terms of a coordinate frame, this becomes

\[\nabla_XY = \left(X(Y^k) + X^iY^j\Gamma^k_{ij}\right)\frac{\partial}{\partial x^k}.\]

Now, recall that the Euclidean connection can be expressed in terms of the standard coordinate frame as follows:

\[\bar{\nabla}_XY = X(Y^j)\frac{\partial}{\partial x^j}.\]

This implies that each of the connection coefficients is \(0\) for the Euclidean connection, i.e. \(\Gamma^k_{ij} = 0\).

Note also that the coordinate expression at a point \(p\) only depends on the value \(X_p\) of \(X\) at \(p\):

\[\nabla_XY\rvert_p = \left(X_p(Y^k) + X^i(p)Y^j(p)\Gamma^k_{ij}(p)\right)\frac{\partial}{\partial x^k}\bigg\rvert_p.\]

Thus, it is possible to define the covariant derivative \(\nabla_vY\rvert_p\) of a vector field \(Y\) along a tangent vector \(v\) at the point \(p\) as \(\nabla_XY\rvert_p\) where \(X\) is any vector field such that \(X_p = v\) defined in some neighborhood of \(p\). In coordinates, we need not even specify the vector field \(X\), since all that matters is the vector \(v\), so we can simply write

\[\nabla_vY\rvert_p = \left(v(Y^k) + v^iY^j(p)\Gamma^k_{ij}(p)\right)\frac{\partial}{\partial x^k}\bigg\rvert_p,\]

where \(v^i\) is the \(i\)-th coordinate for \(v\), i.e. \(v = v^i(\partial/\partial x^i)\rvert_p\) (and \(X^i(p) = v^i\) since \(X_p = v\) and \(X_p = X^i(p)(\partial/\partial x^i)\rvert_p\)).

Symmetric Connections

Recall that the Lie bracket of vector fields is defined as

\[[X,Y]f = XYf - YXf\]

and has coordinate expression

\[[X,Y] = X(Y^j) \frac{\partial}{\partial x^j} - Y(X^j)\frac{\partial}{\partial x^j}.\]

It can be shown that the Lie derivative coincides with the Lie bracket, i.e.

\[[X,Y] = \mathcal{L}_XY.\]

Then, for the Euclidean connection, it follows that

\begin{align}\nabla_XY - \nabla_YX &= X(Y^j)\frac{\partial}{\partial x^j} - Y(X^j)\frac{\partial}{\partial x^j} \\&= [X,Y].\end{align}

For an arbitrary connection,

\begin{align}\nabla_XY - \nabla_YX &= X(Y^j)\frac{\partial}{\partial x^j} + X^iY^j\Gamma^k_{ij}\frac{\partial}{\partial x^k} - Y(X^j)\frac{\partial}{\partial x^j} - X^jY^i\Gamma^k_{ji}\frac{\partial}{\partial x^k} \\&= [X,Y] + \left(X^iY^j\Gamma^k_{ij} - X^jY^i\Gamma^k_{ji}\right) \frac{\partial}{\partial x^k}.\end{align}

If the connection coefficients are symmetric (i.e. \(\Gamma^k_{ij} = \Gamma^k_{ji}\)), then the extra term vanishes, and again \(\nabla_XY - \nabla_YX = [X,Y]\).

The equation

\[\nabla_XY - \nabla_YX = [X,Y]\]

or equivalently

\[\nabla_XY - \nabla_YX - [X,Y] = 0\]

thus provides a coordinate-free way to characterize symmetry. The torsion tensor measures a lack of symmetry:

\[\tau(X,Y) = \nabla_XY - \nabla_YX - [X,Y].\]

For a symmetric connection, \(\tau(X,Y) = 0\). Thus, we can define a symmetric connection as one for which the torsion vanishes identically. Thus, if the connection coefficients are symmetric with respect to every coordinate frame, then the connection will be symmetric (and the converse is also true).

Covariant Derivatives along Curves

One of the main applications of affine connections is to define covariant derivatives along curves, i.e. to define a notion of a derivative of a vector field along a curve. First, we must define a vector field along a curve.

Definition (Vector Field along a Curve). Given a smooth curve \(\gamma : I \rightarrow M\) define on an interval \(I\), a vector field along \(\gamma\) is a continuous map \(V : I \rightarrow TM\) such that \(V(t) \in T_{\gamma(t)}M\) for every \(t \in I\), and it is a smooth vector field along \(\gamma\) if it is smooth as a map from \(I\) to \(TM\). We denote the set of all smooth vector fields along \(\gamma\) as \(\mathfrak{X}(\gamma)\).

Note that \(\mathfrak{X}(\gamma)\) is a real vector space under point-wise addition and multiplication, and a module over \(C^{\infty}(I)\) with multiplication defined as \((fX)(t) = f(t)X(t)\).

An important example of a vector field along a curve is the curve's velocity. Recall that a curve is defined as a continuous map \(\gamma : I \rightarrow M\) from an interval \(I \subseteq \mathbb{R}\) to a smooth manifold \(M\), and a smooth curve is a smooth map \(\gamma : I \rightarrow M\). For any smooth curve \(\gamma\), the velocity of \(\gamma\) at a point \(t_0 \in I\) is denoted \(\gamma'(t_0)\) and defined as follows:

\[\gamma'(t_0) = d\gamma_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right).\]

In other words, if we push the basis tangent vector \((d/dt)\rvert_{t_0}\) forward from \(T_{t_0}I\) to \(T_{\gamma(t_0)}M\), we obtain its velocity. The velocity is also denoted as \(\dot{\gamma}(t_0)\). The velocity thus acts on functions \(f\) by

\begin{align}\gamma'(t_0)(f) &= d\gamma_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)(f) \\&= \frac{d}{dt}\bigg\rvert_{t_0}(f \circ \gamma) \\&= (f \circ \gamma)'(t_0).\end{align}

Thus, the velocity vector acts on a function by computing its derivative along the curve. Given a smooth chart \((U, (x^i))\) on \(M\), the coordinate representation of \(\gamma\) is written as \((\gamma^1(t), \dots, \gamma^n(t))\) where \(\gamma^i(t) = (x^i \circ \gamma)(t)\). Then, the formula for the coordinate representation of the pushforward indicates that

\[\gamma'(t_0) = d\gamma_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right) = \dot{\gamma}^i(t_0)\frac{\partial}{\partial x^i}\bigg\rvert_{t_0},\]

where \(\dot{\gamma}^i(t_0) = (d\gamma^i/dt)(t_0)\).

The coordinate expression indicates that \(\gamma'\) is a smooth vector field along \(\gamma\).

Now, our object is to define the covariant derivative \(D_tV\) of a vector field \(V\) along a curve \(\gamma\). This is intended to be, in some sense, the covariant derivative of \(V\) along the velocity \(\gamma'\). We cannot simply write

\[D_tV = \nabla_{\gamma'}V,\]

since neither \(\gamma'\) nor \(V\) are vector fields (but, rather, are vector fields along the curve \(\gamma\)). As indicated previously, if we have a vector field \(\tilde{V}\), we can interpret the covariant derivative of \(\tilde{V}\) along the tangent vector \(\gamma'(t_0) \in T_{\gamma(t_0)}M\) for any \(t_0 \in I\): simply choose any vector field \(X\) such that \(X_{\gamma(t_0)} = \gamma'(t_0)\) and define \(D_t\tilde{V}(t_0) = \nabla_{\gamma'(t_0)}\tilde{V}\rvert_{\gamma(t_0)} = \nabla_X\tilde{V}\rvert_{\gamma(t_0)}\). In fact, in coordinates, we can directly apply \(\gamma'(t_0)\) without the need for the vector field \(X\). If we select a vector field \(\tilde{V}\) such that \(\tilde{V}_{\gamma(t)} = V(t)\) for all \(t\), then this computes the intended derivative. We thus first make the following preliminary definition.

Definition (Extension of a Vector Field along a Curve). A smooth vector field \(\tilde{V}\) on a neighborhood of the image of a curve \(\gamma : I \rightarrow M\) in a smooth manifold \(M\) is called the extension of a smooth vector field \(V : I \rightarrow TM\) along \(\gamma\) if \(\tilde{V}_{\gamma(t)} = V(t)\) for all \(t \in I\).

Now we are prepared to define the covariant derivative of a vector field along a curve in coordinates. Recall the coordinate representation of the covariant derivative \(\nabla_vY\) for a vector \(v\) at a point \(p\):

\[\nabla_vY\rvert_p = \left(v(Y^k) + v^iY^j(p)\Gamma^k_{ij}(p)\right)\frac{\partial}{\partial x^k}\bigg\rvert_p.\]

Given an extension \(\tilde{V}\) of a vector field \(V\) along a curve \(\gamma\), we then have

\begin{align}\nabla_{\gamma'(t_0)}\tilde{V}\rvert_{\gamma(t_0)} &= \left(\gamma'(t_0)(\tilde{V}^k) + \gamma^i(t_0)\tilde{V}^j(\gamma(t_0))\Gamma^k_{ij}(\gamma(t_0)\right)\frac{\partial}{\partial x^k}\bigg\rvert_{\gamma(t_0)} \\&= \left(\gamma'(t_0)(\tilde{V}^k) + \gamma^i(t_0)V^j(t_0)\Gamma^k_{ij}(\gamma(t_0)\right)\frac{\partial}{\partial x^k}\bigg\rvert_{\gamma(t_0)} \\&= \left((\tilde{V}^k \circ \gamma)'(t_0) + \gamma^i(t_0)V^j(t_0)\Gamma^k_{ij}(\gamma(t_0)\right)\frac{\partial}{\partial x^k}\bigg\rvert_{\gamma(t_0)} \\&= \left(\dot{V}^k(t_0) + \gamma^i(t_0)V^j(t_0)\Gamma^k_{ij}(\gamma(t_0)\right)\frac{\partial}{\partial x^k}\bigg\rvert_{\gamma(t_0)}.\end{align}

The ultimate expression therefore defines the covariant derivative of a vector field along a curve in coordinates:

\[D_tV(t_0) = \left(\dot{V}^k(t_0) + \gamma^i(t_0)V^j(t_0)\Gamma^k_{ij}(\gamma(t_0)\right)\frac{\partial}{\partial x^k}\bigg\rvert_{\gamma(t_0)}.\]

It is possible to provide a coordinate-free definition by abstracting the essential properties of this definition.

Definition (Covariant Derivative along a Curve). Given a smooth manifold \(M\) with an affine connection \(\nabla\) and a smooth curve \(\gamma : I \rightarrow M\), the covariant derivative along \(\gamma\) is an operator

\[D_t : \mathfrak{X}(\gamma) \rightarrow \mathfrak{X}(\gamma)\]

that satisfies the following properties:

• Linearity over \(\mathbb{R}\):
  • \(D_t(aV) =aD_tV\) for all \(a \in \mathbb{R}\) and \(V \in \mathfrak{X}(\gamma)\),
  • \(D_t(V+W) = D_tV + D_tW\) for all \(V,W \in \mathfrak{X}(\gamma)\),
• Product rule: \(D_t(fV) = f'V + dD_tV\) for all \(f \in C^{\infty}(I)\) and \(V \in \mathfrak{X}(\gamma)\),
• Whenever \(V\) admits an extension \(\tilde{V}\), \(D_tV(t_0) = \nabla_{\gamma'(t_0)}\tilde{V}\rvert_{\gamma(t_0)}\).

The coordinate definition above satisfies each of these properties, and it can be shown that it is unique.

Geodesics

A geodesic is a generalization of the concept of the shortest path between two points (i.e. a straight line) in Euclidean space. The term "geodesic" derives from the study of geodesy, the measurement of the size and shape of the Earth, where geodesics are the shortest paths along the surface of the Earth. Intuitively, the shortest path should have zero acceleration. Now that we have a notion of the covariant derivative of a vector field along a curve, we can define the acceleration of a curve as the covariant derivative of the curve's velocity.

Definition (Acceleration of a Curve). The acceleration of a smooth curve \(\gamma: I \rightarrow M\) in a smooth manifold \(M\) is the following vector field along \(\gamma\):

\[D_t\gamma'.\]

A geodesic is then a smooth curve with zero acceleration.

Definition (Geodesic). A smooth curve \(\gamma: I \rightarrow M\) defined on a smooth manifold \(M\) is a geodesic if

\[D_t\gamma' = 0.\]

Writing the component functions in terms of smooth coordinates \((x^i)\) as

\[\gamma(t) = (\gamma^1(t), \dots, \gamma^n(t)),\]

and using the coordinate expression for the covariant derivative of a vector field along a curve derived above, we obtain the following expression for the acceleration of a curve in coordinates

\[\left(\ddot{\gamma}^k(t) + \dot{\gamma}^i(t)\dot{\gamma}^j(t)\Gamma^k_{ij}(\gamma(t)\right)\frac{\partial}{\partial x^k}\bigg\rvert_{\gamma(t)}.\]

It then follows that a curve is a geodesic if and only if the following equation, called the geodesic equation, is satisfied:

\[\ddot{\gamma}^k(t) + \dot{\gamma}^i(t)\dot{\gamma}^j(t)\Gamma^k_{ij}(\gamma(t)) = 0.\]

Parallel Transport

More generally, we can say that a vector field \(V\) along a curve \(\gamma\) is parallel along \(\gamma\) if \(D_tV = 0\), which intuitively means that the "rate of change" of the vector field is \(0\), i.e. the corresponding tangent vectors in each tangent space remain "constant" in a certain sense. Thus, a geodesic is a curve whose velocity vector field is a parallel along the curve.

Definition (Parallel Vector Field along a Curve). A vector field \(V\) along a curve \(\gamma\) is parallel along \(\gamma\) if \(D_tV = 0\).

The following theorem can be demonstrated:

Theorem (Existence and Uniqueness of Parallel Transport). For any smooth curve \(\gamma : I \rightarrow M\) on a smooth manifold \(M\) with affine connection \(\nabla\), point \(t_0 \in I\), and tangent vector \(v \in T_{\gamma(t_0)}M\), there exists a unique parallel vector field along \(\gamma\), called the parallel transport of \(v\) along \(\gamma\), such that \(V(t_0) = v\).

We will not prove this here, since it would involve an excursion. However, we will demonstrate that parallel transport determines the connection and vice versa.

The parallel transport thus "transports" a tangent vector \(v\) in a "parallel" manner along a curve. The parallel transport is the mechanism by which a connection "connects" tangent spaces.

Parallel transport induces a map

\[P^{\gamma}_{t_0,t_1} : T_{\gamma(t_0)}M \rightarrow T_{\gamma(t_1)}M,\]

called the parallel transport map, such that

\[P^{\gamma}_{t_0,t_1}(v) = V(t_1)\]

for all \(t_1 \in I\), where \(V\) is the parallel transport of \(v\) along \(\gamma\). This map is a linear isomorphism (whose inverse is the map \(P^{\gamma}_{t_1,t_0}\)).

We can also define the concept of a parallel frame along a curve. Given any basis \(e_1,\dots,e_n\) for the tangent space \(T_{\gamma(t_0)}M\), it is possible to parallel transport the basis vectors \(e_i\) along the curve \(\gamma\). This induces a tuple of parallel vector fields \((E_1, \dots, E_n)\) along \(\gamma\). Since the parallel transport map is a linear isomorphism, the vectors \((E_i(t))\) form a basis for the tangent space \(T_{\gamma(t)}M\) at each point \(\gamma(t)\) along \(\gamma\). This tuple is called a parallel frame along \(\gamma\). Thus, every smooth vector field \(V\) along \(\gamma\) can be expressed in terms of this parallel frame as \(V(t) = V^i(t)E_i(t)\). Furthermore, it follows that

\begin{align}D_tV(t_0) &= D_t\left(V^i(t_0)E_i(t_0)\right) \\&= \dot{V}^i(t_0)E_i(t_0) + V^i(t_0)D_tE_i(t_0) & \text{(product rule)} \\&= \dot{V}^i(t_0)E_i(t_0) & \text{(since each \(E_i\) is parallel along \(\gamma\))}\end{align}

Thus, a vector field \(V\) along a curve \(\gamma\) is parallel if and only if each of its component functions \(V^i\) are constant (and hence \(\dot{V}^i = 0\), making \(D_tV = \dot{V}^i(t_0)E_i(t_0) = 0\)). Thus, since the component functions are constant, it follows that \(V^i(t_1) = V^i(t_0)\), and we may therefore write

\[P^{\gamma}_{t_1,t_0}V(t_1) = V^i(t_1)E_i(t_1) = V^i(t_0)E_i(t_1).\]

Now, by definition

\[\dot{V}^i(t_0) = \lim_{t_1 \to 0}\frac{V^i(t_0 + t_1) - V^i(t_0)}{t_1}.\]

Since limits in normed vector spaces can be "translated" i.e.

\[\lim_{h \to a}f(h-a) = \lim_{h \to 0}f(h),\]

it follows that

\[\dot{V}^i(t_0) = \lim_{t_1 \to t_0}\frac{V^i(t_1) - V^i(t_0)}{t_1 - t_0}.\]

Futhermore, since limits in normed vector spaces are computed component-wise, it follows that

\[\left[\lim_{t_1 \to t_0}\frac{V^i(t_1) - V^i(t_0)}{t_1 - t_0}\right] \cdot E_i(t_0) = \lim_{t_1 \to t_0}\left[\frac{V^i(t_1) - V^i(t_0)}{t_1 - t_0} \cdot E_i(t_0)\right]\]

and thus

\[\dot{V}^i(t_0)E_i(t_0) = \lim_{t_1 \to t_0}\left[\frac{V^i(t_1) - V^i(t_0)}{t_1 - t_0} \cdot E_i(t_0)\right].\]

This is equivalent to

\[\dot{V}^i(t_0)E_i(t_0) = \lim_{t_1 \to t_0}\frac{V^i(t_1) E_i(t_0) - V^i(t_0)E_i(t_0)}{t_1 - t_0}\]

which is again equivalent to

\[\dot{V}^i(t_0)E_i(t_0) = \lim_{t_1 \to t_0}\frac{P^{\gamma}_{t_1,t_0}V(t_1) - V(t_0)}{t_1 - t_0}.\]

It thus follows that

\[D_tV(t_0) = \lim_{t_1 \to t_0}\frac{P^{\gamma}_{t_1,t_0}V(t_1) - V(t_0)}{t_1 - t_0}.\]

Thus, the parallel transport determines the covariant derivative along a curve.

Furthermore, consider a smooth manifold \(M\) and smooth vector fields \(X\) and \(Y\) on \(M\) and suppose that \(\gamma : I \rightarrow M\) is a smooth curve such that \(\gamma(0) = p\) and \(\gamma'(0) = X_p\) at a point \(p \in M\). Let \(V(t)\) denote the vector field along \(\gamma\) determined by \(Y\), i.e. \(Y\) is the extension of \(V(t)\), that is, \(V(t) = Y_{\gamma(t)}\) for all \(t \in I\). Then, by one of the defining properties of covariant derivatives of vector fields along curves, it follows that

\begin{align}D_tV(0) &= \nabla_{\gamma'(0)}Y\rvert_{\gamma(0)} \\&= \nabla_{X_p}Y\rvert_p \\&= \nabla_XY\rvert_p.\end{align}

Then, as we just established, it follows that

\begin{align}D_tV(0) &= \lim_{t \to 0}\frac{P^{\gamma}_{t,0}V(t) - V(0)}{t} \\&= \lim_{t \to 0}\frac{P^{\gamma}_{t,0}Y_{\gamma(t)} - Y_{\gamma(0)}}{t} \\&= \lim_{t \to 0}\frac{P^{\gamma}_{t,0}Y_{\gamma(t)} - Y_p}{t} .\end{align}

Thus, the parallel transport determines the covariant derivative, and hence the connection. Thus, connections and parallel transport are equivalent in this sense. This justifies the terminology "connection".

Metric Connections

Recall that the Euclidean inner product (dot product) is defined as follows for any \(v,w \in \mathbb{R}^n\):

\[\langle v, w \rangle = \sum_{i=1}^n v^iw^i.\]

Given any two vector fields \(X,Y : \mathbb{R}^n \rightarrow \mathbb{R}^n\), their inner product is the function defined as follows for each \(p \in \mathbb{R}^n\):

\[\langle X, Y \rangle(p) = \langle X(p), Y(p) \rangle.\]

Now, consider the following:

\begin{align}(\bar{\nabla}_X\langle Y,Z \rangle)(p) &= \frac{d}{dt}\bigg\rvert_0 \langle Y,Z \rangle(p + t \cdot X(p)) \\&= \frac{d}{dt}\bigg\rvert_0 \left\langle Y(p + t \cdot X(p)), Z(p + t \cdot X(p))\right\rangle \\&= \frac{d}{dt}\bigg\rvert_0 \sum_{j=1}^n \left(Y^j(p + t \cdot X(p)) \cdot Z^j(p + t \cdot X(p))\right) \\&= \sum_{j=1}^n \frac{d}{dt}\bigg\rvert_0 \left(Y^j(p + t \cdot X(p)) \cdot Z^j(p + t \cdot X(p)) \right) \\&= \sum_{j=1}^n \left[Z^j(p + t \cdot X(p))\rvert_0 \cdot \left(\frac{d}{dt}\bigg\rvert_0[Y^j(p + t \cdot X(p))\right) + Y^j(p + t \cdot X(p))\rvert_0 \cdot \left(\frac{d}{dt}\bigg\rvert_0 Z^j(p + t \cdot X(p))\right)\right] \\&= \sum_{j=1}^n \left[Z^j(p) \cdot \left(\frac{d}{dt}\bigg\rvert_0[Y^j(p + t \cdot X(p))\right) + Y^j(p) \cdot \left(\frac{d}{dt}\bigg\rvert_0 Z^j(p + t \cdot X(p))\right)\right] \\&= \sum_{j=1}^n \left[Z^j(p) \cdot X^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) + Y^j(p) \cdot X^i(p) \cdot \frac{\partial Z^j}{\partial x^i}(p)\right] \\&= \sum_{j=1}^n \left[Z^j(p) \cdot X^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p)\right] + \sum_{j=1}^n \left[Y^j(p) \cdot X^i(p) \cdot \frac{\partial Z^j}{\partial x^i}(p)\right] \\&= \left\langle Z^j(p) \cdot e_j, X^i(p) \cdot \frac{\partial Y^j}{\partial x^i}(p) \cdot e_j\right\rangle + \left\langle Y^j(p) \cdot e_j, \cdot X^i(p) \cdot \frac{\partial Z^j}{\partial x^i}(p) \cdot e_j\right\rangle \\&= \langle Z(p), (\bar{\nabla}_XY)(p) \rangle + \langle Y(p), (\bar{\nabla}_XZ)(p) \rangle \\&= \langle \bar{\nabla}_XY, Z \rangle(p) + \langle Y, \bar{\nabla}_XZ \rangle(p).\end{align}

Thus, the Euclidean connection obeys the following product rule relative to the Euclidean inner product:

\[\bar{\nabla}_X\langle Y,Z \rangle = \langle \bar{\nabla}_XY, Z\rangle + \langle Y, \bar{\nabla}_XZ \rangle.\]

We thus make the following definition for an arbitrary Riemannian or semi-Riemannian manifold:

Definition (Metric Connection). A connection \(\nabla\) on a smooth manifold \(M\) with semi-Riemannian metric \(g = \langle -,-\rangle\) is a metric connection (or is compatible with the metric) if, for all \(X,Y,Z \in \mathfrak{X}(M)\), the following product rule is satisfied:

\[\nabla_X\langle Y,Z \rangle = \langle \nabla_XY, Z\rangle + \langle Y, \nabla_XZ \rangle.\]

Next, we will demonstrate that every Riemannian (or semi-Riemannian) manifold admits a unique symmetric metric connection. First note that, for any metric connection \(\nabla\), it follows that

• \[\nabla_X\langle Y,Z \rangle = X\langle Y,Z \rangle = \langle \nabla_XY, Z \rangle + \langle Y, \nabla_XZ \rangle,\]
• \[\nabla_Y\langle Z,X \rangle = Y\langle Z,X \rangle = \langle \nabla_YZ, X \rangle + \langle Z, \nabla_YX \rangle,\]
• \[\nabla_Z\langle X,Y \rangle = Z\langle X,Y \rangle = \langle \nabla_ZX, Y \rangle + \langle X, \nabla_ZY \rangle.\]

This computes each permutation of the action. Now, if the connection is furthermore symmetric, then it follows that

• \[\nabla_XZ = \nabla_ZX + [X,Z],\]
• \[\nabla_YX = \nabla_XY + [Y,X],\]
• \[\nabla_ZY = \nabla_YZ + [Z,Y].\]

Substituting these expressions into the ultimate terms of each of the previous expressions, we obtain

• \[X\langle Y,Z \rangle = \langle \nabla_XY, Z \rangle + \langle Y, \nabla_ZX \rangle + \langle Y, [X,Z] \rangle,\]
• \[Y\langle Z,X \rangle = \langle \nabla_YZ, X \rangle + \langle Z, \nabla_XY \rangle + \langle Z, [Y,X] \rangle,\]
• \[Z\langle X,Y \rangle = \langle \nabla_ZX, Y \rangle + \langle X, \nabla_YZ \rangle + \langle X, [Z,Y] \rangle.\]

Our goal is to isolate an expression for \(\langle \nabla_XY,Z \rangle\), so we add the first two equations and subtract the third equation, which yields

\[X\langle Y,Z \rangle + Y\langle Z,X \rangle - Z\langle X,Y \rangle = 2 \cdot \langle \nabla_XY, Z \rangle + \langle Y, [X,Z] \rangle + \langle X, [Z,Y] \rangle.\]

Finally, solving for \(\langle \nabla_XY, Z \rangle\) yields

\[\langle \nabla_XY,Z \rangle = \frac{1}{2} \cdot \left(X\langle Y,Z \rangle + Y\langle Z,X \rangle - Z\langle X,Y \rangle - \langle Y, [X,Z] \rangle - \langle Z, [Y,X] \rangle + \langle X, [Z,Y] \rangle\right).\]

Now, note that the right-hand side of this equation does not depend on the connection in any way (i.e. it does not contain any term involving \(\nabla\)). Thus, if \(\nabla^1\) and \(\nabla^2\) are both symmetric connections compatible with the metric, then it follows that they will each be equal to this right-hand side, and thus

\[\langle \nabla^1_XY, Z \rangle = \langle \nabla^2_XY,Z \rangle,\]

or equivalently

\[\langle \nabla^1_XY, Z \rangle - \langle \nabla^2_XY,Z \rangle = 0.\]

Since the metric is bilinear by definition, it follows that

\[\langle \nabla^1_XY - \nabla^2_XY, Z \rangle = 0.\]

Since this is true for all \(Z\) and the metric is non-degenerate by definition, it follows that

\[\nabla^1_XY - \nabla^2_XY = 0\]

and hence

\[\nabla^1_XY = \nabla^2_XY,\]

so \(\nabla^1 = \nabla^2\). Thus, if a semi-Riemannian manifold admits a symmetric connection that is compatible with the metric, then this connection is necessarily unique.

Next, we will demonstrate the existence of such a connection. Let \((U,(x^i))\) be any smooth coordinate chart. First note that the Lie bracket of coordinate vector fields is always \(0\):

\[\left[\frac{\partial}{\partial x^i}, \frac{\partial}{\partial x^j}\right] = 0.\]

Next, we will use the notation

\[\partial_i = \frac{\partial}{\partial x^i}.\]

We then apply the expression derived above to a triple of coordinate vector fields \(\partial_i\), \(\partial_j\), and \(\partial_l\) (noting that the Lie brackets will be \(0\)):

\[\langle \nabla_{\partial_i}\partial_j,\partial_k \rangle = \frac{1}{2} \cdot \left(\partial_i\langle \partial_j, \partial_l \rangle + \partial_j\langle \partial_l,\partial_i \rangle - \partial_ \langle \partial_i,\partial_j \rangle\right).\]

Recall that, by definition, for a metric \(g = \langle -,- \rangle\), the coefficient functions of the metric are computed by applying the metric to pairs of coordinate vector fields as follows:

\[g_{ij} = \langle \partial_i, \partial_j \rangle.\]

Also recall that these coefficients can be arranged into an \(n \times n\) square matrix \(g_{ij}\) (where \(n = \mathrm{dim}(M)\)) so that, for any vector fields \(X\) and \(Y\) with component functions \(X^i\) and \(Y^i\), respectively,

\[\langle X,Y \rangle = g_{ij} X^i Y^j.\]

Note that, since the component functions of each coordinate vector field \(\partial_j\) are constant, namely \(\partial^j_k = 0\) when \(j \neq k\) and \(\partial^j_k = 1\) when \(j=k\), i.e. \(\partial^j_k = \delta^j_k\) where \(\delta^j_k\) is the Kronecker delta function, it follows that

\[\langle X,\partial_k \rangle = g_{ij} X^i \partial^j_k = g_{ij} X^i \delta^j_k = g_{ik}X^i.\]

Further recall that we previously determined that the connection coefficients are expressed as

\[\nabla_{\partial_i}\partial_j = \Gamma^m_{ij}\partial_m.\]

We then compute

\[\langle \nabla_{\partial_i}\partial_j, \partial_l \rangle = g_{ml} \cdot \Gamma^m_{ij}.\]

Combining equations, we obtain

\[ g_{ml} \cdot \Gamma^m_{ij} = \frac{1}{2} \cdot \left(\partial_ig_{jl} + \partial_jg_{il} - \partial_lg_{ij}\right).\]

We solve for the connection coefficients \(\Gamma^m_{ij}\) by multiplying by the inverse of the matrix \(g_{ml}\) which is the matrix \(g^{kl}\) such that

\[g_{ml} \cdot g^{kl} = \delta^k_m,\]

where \(\delta^k_m\) is the Kronecker delta function defined such that \(\delta^k_m = 1\) when \(k=m\) and \(0\) otherwise (i.e. it represents the identity matrix). Recall that, since the metric is a symmetric tensor field, it follows that the matrix \(g^{kl}\) is symmetric, and hence \(g^{kl} = g^{lk}\). Thus, multiplying both sides of the equation by the inverse matrix, we obtain

\[ \Gamma^k_{ij} = \frac{1}{2} g^{kl} \left(\partial_ig_{jl} + \partial_jg_{il} - \partial_lg_{ij}\right).\]

These connection coefficients are called the Christoffel symbols.

By the symmetry of the matrices, it follows that

\[\Gamma^{k}_{ij} = \Gamma^{k}_{ji},\]

and hence a connection defined by these coefficient functions is a symmetric connection.

Next, we will confirm that such a connection is indeed a metric connection. First note that

\begin{align}\langle \nabla_XY,Z\rangle &= \langle \nabla_{X^i\partial_i}(Y^j\partial_j),Z^l\partial_l\rangle \\&= X^iZ^l\langle \nabla_{\partial_i}(Y^j\partial_j), \partial_l\rangle \\&= X^iZ^l\langle Y^j \nabla_{\partial_i}\partial_j + (\partial_iY^j)\partial_j,\partial_l\rangle \\&= X^iY^jZ^l \langle \nabla_{\partial_i}\partial_j,\partial_l\rangle + X^i(\partial_iY^j)Z^l\langle \partial_j, \partial_l\rangle \\&= X^iY^jZ^l\left[\frac{1}{2}(\partial_ig_{jl} + \partial_jg_{il} - \partial_lg_{ij})\right] + g_{jl}X^i(\partial_iY^j)Z^l.\end{align}

Next, note that

\begin{align}\langle Y, \nabla_XZ\rangle &= \langle Y^j\partial_j,\nabla_{X^i\partial_i}Z^l\partial_l\rangle \\&= X^iY^j\langle \partial_j,\nabla_{\partial_i}(Z^l\partial_l)\rangle \\&= X^iY^j\langle \partial_j, \rangle Z^l \nabla_{\partial_i}\partial_l + (\partial_iZ^l)\partial_l\rangle \\&= X^iY^jZ^l\langle \partial_j, \nabla_{\partial_i}\partial_l\rangle + X^iY^j(\partial_iZ^l)\langle \partial_j,\partial_l\rangle \\&= X^iY^jZ^l\left[\frac{1}{2}(\partial_ig_{lj} + \partial_lg_{ij} - \partial_jg_{il})\right] + g_{jl}X^iY^j(\partial_iZ^l).\end{align}

Then, note that

\begin{align}\nabla_X\langle Y,Z\rangle &= X\langle Y,Z\rangle \\&= X^i\partial_i(g_{jl}Y^jZ^l) \\&= X^i(g_{jl}\partial_i(Y^jZ^l) + Y^jZ^l\partial_ig_{jl}) \\&= X^i(g_{jl}Y^j\partial_iZ^l + g_{jl}Z^l\partial_iY^j + Y^jZ^l\partial_ig_{jl}) \\&= g_{jl}X^iY^j(\partial_iZ^l) + g_{jl}X^i(\partial_iY^j)Z^l + X^iY^jZ^l\partial_ig_{jl}. \end{align}

Finally, note that these equations imply that

\[\nabla_X\langle Y,Z\rangle = \langle \nabla_XY,Z\rangle + \langle Y,\nabla_XZ\rangle.\]

Thus, such a connection is indeed compatible with the metric.

Although this defines the connection only on individual charts, since this connection is unique, it follows that the connections agree on all chart overlaps.

This connection is called the Levi-Civita connection. The existence and uniquess of the Levi-Civita connection is called the fundamental theorem of Riemannian geometry.

Generalizations

In this post, only "affine" connections on the tangent bundle were discussed. However, the notion of connection defined above makes sense in any vector bundle defined on a smooth manifold, not just the tangent bundle. Furthermore, there are other notions of connections. The type of connection discussed in this post is often called a Koszul connection. Another type of connection is an Ehresmann connection, which makes use of the theory of fiber bundles.