Differentiable Programming

Differentiable programming refers to the systematic use of a technique called automatic differentiation to compute the derivatives of a numeric computer program (a program represented by a continuous function \(f : \mathbb{R}^n \rightarrow \mathbb{R}^m\)). One prominent application of differentiable programming is within deep learning, where, for instance, the derivatives of a numeric program representing an artificial neural network are used for optimizing the network with respect to some loss function. This is the approach implemented in popular frameworks such as PyTorch, JAX, and TensorFlow. This technique permits derivatives to be computed automatically for arbitrarily complex expressions, which obviates the need for programmers to explicitly calculate them for each expression (and even permits the expressions to vary dynamically), and significantly simplifies the programming task.

First, let's begin with a brief review of elementary differential geometry (calculus on manifolds). In particular, the concepts of pushforwards, pullbacks, and the chain rule are relevant to our discussion. The following posts provide further detail:

• total derivatives
• smooth manifolds
• tangent spaces
• cotangent spaces

Pushforwards

Given a smooth map \(F : M \rightarrow N\) between smooth manifolds \(M\) and \(N\), the pushforward \(dF_p : T_pM \rightarrow T_pN\) of \(F\) at the point \(p \in M\) (also called the total derivative or differential) is defined, for each tangent vector \(v \in T_pM\) and each smooth function \(f \in C^{\infty}(N)\), to be the following linear map:

\[dF_p(v)(f) = v(f \circ F).\]

Chain Rule

The pushforward satisfies the following chain rule: for any smooth maps \(F : M \rightarrow N\) and \(G : N \rightarrow P\) between smooth manifolds \(M\), \(N\), and \(P\), any point \(p \in M\), any tangent vector \(v \in T_pM\), and any smooth function \(f \in C^{\infty}(M\)),

\begin{align}d(G \circ F)_p(v)(f) &= v(f \circ (G \circ F)) \\&= v((f \circ G) \circ F) \\&= dF_p(v)(f \circ G) \\&= dG_{F(p)}(dF_p(v))(f) \\&= (dG_{F(p)} \circ dF_p)(v)(f).\end{align}

Thus, it follows that

\[d(G \circ F)_p = dG_{F(p)} \circ dF_p.\]

Tangent Vectors

Each tangent vector \(v \in T_pM\) is defined to be a derivation at the point \(p\), i.e. a map \(v : C^{\infty}(M) \rightarrow \mathbb{R}\) linear over \(\mathbb{R}\) which satisfies the following product rule for each \(f,g \in C^{\infty}(M)\):

\[v(fg) = f(p)v(g) + g(p)v(f).\]

Thus, tangent vectors are defined by how they act; they act by computing the respective directional derivative of smooth functions, so they are operators that map smooth functions to directional derivatives. Derivations abstract the essential properties of such mappings, and the set of directional derivative operators at a point is isomorphic to the set of derivations at a point, so derivations are taken as the definition of tangent vectors.

Coordinate Basis Vectors

For each smooth function \(f \in C^{\infty}(\mathbb{R}^n)\), the following map, called the coordinate basis vector (on \(\mathbb{R}^n\)), is a derivation at each point \(p \in (\mathbb{R}^n)\):

\[\frac{\partial}{\partial x^i}\bigg\rvert_p(f) = \frac{\partial f}{\partial x^i}(p),\]

where \(x^i\) denotes the \(i\)-th coordinate function relative to the standard basis on \(\mathbb{R}^n\) and \((\partial f/\partial x^i)(p)\) denotes the partial derivative of \(f\) with respect to \(x^i\).

Given a smooth coordinate chart \((U, \varphi)\) on a smooth manifold \(M\), we can define a related derivation called a coordinate basis vector (on \(T_pM\)) at each point \(p \in M\) as follows:

\[\frac{\partial}{\partial x^i}\bigg\rvert_p = d(\varphi^{-1})_{\varphi(p)}\left(\frac{\partial}{\partial x^i}\bigg\rvert_{\varphi(p)}\right),\]

where \(f \in C^{\infty}(U)\). This tangent vector thus acts as follows:

\[\frac{\partial}{\partial x^i}\bigg\rvert_p(f) = \frac{\partial \hat{f}}{\partial x^i}(\hat{p}),\]

where \(\hat{f} = f \circ \varphi^{-1}\) is the coordinate representation of \(f\) and \(\hat{p} = \varphi(p)\) is the coordinate representation of \(p\). The notation for the coordinate basis vectors on \(\mathbb{R}^n\) and \(T_pM\) is deliberately conflated since they are closely related.

Thus, each derivation \(v \in T_pM\) can be represented as a linear combination of such coordinate basis vectors:

\[v = v^i \frac{\partial}{\partial x^i}\bigg\rvert_p.\]

In particular, the coordinates are calculated as follows:

\[v^i = v(x^i).\]

Tangent Space

The tangent space \(T_pM\) at the point \(p \in M\) is the vector space of all derivations at the point \(p\). The derivations \((\partial/\partial x^i \rvert_p)\) form a basis for \(T_pM\), called the coordinate basis.

Pushforward in Coordinates

We can examine the action of the pushforward of a smooth map \(F : \mathbb{R}^n \rightarrow \mathbb{R}^m\) in coordinates by computing its action on the coordinate expression of an arbitrary tangent vector \(v = v^i(\partial/\partial x^i\rvert_p)\) at a point \(p \in \mathbb{R}^n\), where \((x^i)\) are the coordinate functions in \(\mathbb{R}^n\) and \((y^i)\) are the coordinate functions in \(\mathbb{R}^m\) as follows:

\begin{align}dF_p\left(v^i\frac{\partial}{\partial x^i}\bigg\rvert_p\right) &= dF_p\left(v^i\frac{\partial}{\partial x^i}\bigg\rvert_p\right)(y^j)\frac{\partial}{\partial y^j}\bigg\rvert_{F(p)}\\&= v^i\frac{\partial}{\partial x^i}\bigg\rvert_p (y^j \circ F)\frac{\partial}{\partial y^j}\bigg\rvert_{F(p)} \\&= v^i\frac{\partial}{\partial x^i}\bigg\rvert_p (F^j)\frac{\partial}{\partial y^j}\bigg\rvert_{F(p)} \\&= v^i\frac{\partial F^j}{\partial x^i}(p)\frac{\partial}{\partial y^j}\bigg\rvert_{F(p)}\end{align}

Thus, the vector with components \((v^i)\) in \(\mathbb{R}^n\) is mapped to the vector \((\bar{v}^j)\) with components \(\bar{v}^j = v^i\frac{\partial F^j}{\partial x^i}(p)\) in \(\mathbb{R}^m\), and this mapping can be expressed using matrix multiplication as follows:

\[\begin{bmatrix}\frac{\partial F^1}{\partial x^1}(p) & \dots & \frac{\partial F^1}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^m}{\partial x^1}(p) & \dots & \frac{\partial F^m}{\partial x^n}(p)\end{bmatrix}\begin{bmatrix}v^1 \\ \vdots \\ v^n\end{bmatrix} = \begin{bmatrix}v^i\frac{\partial F^1}{\partial x^i}(p) \\ \vdots \\ v^i\frac{\partial F^m}{\partial x^i}(p)\end{bmatrix}\]

Jacobian Matrix

This \(m \times n\) matrix, which represents the pushforward \(dF_p\) in coordinates, is called the Jacobian matrix, and is denoted \(DF\):

\[DF = \begin{bmatrix}\frac{\partial F^1}{\partial x^1}(p) & \dots & \frac{\partial F^1}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^m}{\partial x^1}(p) & \dots & \frac{\partial F^m}{\partial x^n}(p)\end{bmatrix}.\]

Thus, for row \(i\) and column \(j\),

\[(DF)_{ij} = \left(\frac{\partial F^i}{\partial x^j}(p)\right).\]

The chain rule then implies for smooth maps \(F : \mathbb{R}^n \rightarrow \mathbb{R}^m\) and \(G : \mathbb{R}^m \rightarrow \mathbb{R}^l\) that the matrix which represents \(d(G \circ F)_p\) is the \(l \times n\) matrix \(D(G \circ F) = (DG)(DF)\), so that

\begin{align}D(G \circ F) &= \begin{bmatrix}\frac{\partial G^1}{\partial y^1}(F(p)) & \dots & \frac{\partial G^1}{\partial y^n}(F(p)) \\ \vdots & \ddots & \vdots \\ \frac{\partial G^l}{\partial y^1}(F(p)) & \dots & \frac{\partial G^l}{\partial y^n}(F(p))\end{bmatrix}\begin{bmatrix}\frac{\partial F^1}{\partial x^1}(p) & \dots & \frac{\partial F^1}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^m}{\partial x^1}(p) & \dots & \frac{\partial F^m}{\partial x^n}(p)\end{bmatrix} \\&= \begin{bmatrix}\frac{\partial G^1}{\partial y^i}(F(p))\frac{\partial F^i}{\partial x^1}(p) & \dots & \frac{\partial G^1}{\partial y^i}(F(p))\frac{\partial F^i}{\partial x^n}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial G^m}{\partial y^i}(F(p))\frac{\partial F^i}{\partial x^1}(p) & \dots & \frac{\partial G^m}{\partial y^i}(F(p))\frac{\partial F^i}{\partial x^n}(p)\end{bmatrix}.\end{align}

Thus, the matrix \(D(G \circ F)\) can be summarized for row \(i\) and column \(j\) as

\[D(G \circ F)_{ij} = \left(\frac{\partial G^i}{\partial y^k}(F(p))\frac{\partial F^k}{\partial x^j}(p)\right).\]

This can be confirmed by calculating using the chain rule directly:

\begin{align}d(G \circ F)_p\left(\frac{\partial}{\partial x^j}\bigg\rvert_p\right) &= (dG_{F(p)} \circ dF_p)\left(\frac{\partial}{\partial x^j}\bigg\rvert_p\right) \\&= dG_{F(p)}\left(dF_p\left(\frac{\partial}{\partial x^j}\bigg\rvert_p\right)\right) \\&= dG_{F(p)}\left(dF_p\left(\frac{\partial}{\partial x^j}\bigg\rvert_p\right)(y^k)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}\right) \\&= dG_{F(p)}\left(\frac{\partial}{\partial x^j}\bigg\rvert_p(y^k \circ F)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}\right) \\&= dG_{F(p)}\left(\frac{\partial}{\partial x^j}\bigg\rvert_p(F^k)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}\right) \\&= dG_{F(p)}\left(\frac{\partial F^k}{\partial x^j}(p)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}\right) \\&= dG_{F(p)}\left(\frac{\partial F^k}{\partial x^j}(p)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}\right)(z^i)\frac{\partial}{\partial z^i}\bigg\rvert_{G(F(p))} \\&= \frac{\partial F^k}{\partial x^j}(p)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}(z^i \circ G)\frac{\partial}{\partial z^i}\bigg\rvert_{G(F(p))} \\&= \frac{\partial F^k}{\partial x^j}(p)\frac{\partial}{\partial y^k}\bigg\rvert_{F(p)}(G^i)\frac{\partial}{\partial z^i}\bigg\rvert_{G(F(p))} \\&= \frac{\partial F^k}{\partial x^j}(p)\frac{\partial G^i}{\partial y^k}(F(p))\frac{\partial}{\partial z^i}\bigg\rvert_{G(F(p))}.\end{align}

Pullbacks

Given a smooth map \(F: M \rightarrow N\) between smooth manifolds \(M\) and \(N\), the (pointwise) pullback along \(F\) at the point \(p \in M\) is defined to be the dual \(dF^*_p : T^*_{F(p)}N \rightarrow T^*_pM\) of the (pointwise) pushforward \(dF_p\), that is, the linear map defined for each cotangent vector \(\omega \in T^*_{F(p)}N\) and tangent vector \(v \in T_pM\) as follows:

\[dF^*_p(\omega)(v) = \omega\left(dF_p(v)\right).\]

This is equivalent to the following definition:

\[df^*_p(\omega) = \omega \circ dF_p.\]

Chain Rule

The pullback satisfies the following dual of the chain rule: for any smooth maps \(F : M \rightarrow N\) and \(G : N \rightarrow P\) and any cotangent vector \(\omega \in T_{G(F(p))}P\),

\begin{align}d(G \circ F)^*_p(\omega) &= \omega \circ d(G \circ F)_p \\&= \omega \circ dG_{F(p)} \circ dF_p \\&= dG^*_{F(p)}(\omega) \circ dF_p \\&= dF^*_p\left(dG^*_{F(p)}(\omega)\right) \\&= \left(dF^*_p \circ dG^*_{F(p)}\right)(\omega).\end{align}

Cotangent Vectors

Each cotangent vector \(\omega \in T^*_pM\) is defined to be a dual tangent vector, i.e. a linear map \(\omega : T_pM \rightarrow \mathbb{R}\).

Dual Coordinate Basis Vectors

For each smooth function \(f \in C^{\infty}(M)\), the differential \(df_p\) of \(f\) at the point \(p \in M\) on a smooth manifold \(M\) is defined, for each tangent vector \(v \in T_pM\), to be the following linear map:

\[df_p(v) = v(f).\]

The terminology "differential" is thus used both for the pointwise pushforward \(dF_p : T_pM \rightarrow T_{F(p)}\mathbb{R}\) of a smooth map \(F : M \rightarrow \mathbb{R}\) and for the differential \(df_p : T_pM \rightarrow \mathbb{R}\) of a smooth, real-valued function \(f\). These definitions coincide for smooth maps \(F : M \rightarrow \mathbb{R}\) since there is a canonical isomorphism \(T_{F(p)}\mathbb{R} \cong \mathbb{R}\) between the tangent space \(T_{F(p)}\mathbb{R}\) and the space \(\mathbb{R}\).

Given smooth coordinates \((x^i)\) on \(M\), the differentials \(dx^i\rvert_p\) of the coordinate functions comprise a basis for the cotangent space \(T^*_pM\), and thus each cotangent vector \(\omega \in T^*_pM\) can be represented as a linear combination of such differentials:

\[\omega = \omega_i dx^i\rvert_p.\]

In particular, each component \(\omega_i\) can be calculated as follows

\[\omega_i = \omega\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right).\]

This is because, for any vector space \(V\) with basis \((E_i)\), the components of each dual vector \(\omega \in V^*\) are computed relative to the corresponding dual basis \((\varepsilon^i)\) as \(\omega_i = \omega(E_i)\) so that \(\omega = \omega_i\varepsilon^i\). Then, given any coordinate functions \((x^i)\) and dual coordinate basis \((\lambda_i\lvert_p)\),

\begin{align}dx^j\lvert_p &= dx^j\lvert_p\left(\frac{\partial}{\partial x^i}\bigg\lvert_p\right)\lambda^i\lvert_p \\&= \frac{\partial x^j}{\partial x^i}(p)\lambda_i\lvert_p \\&= \delta^j_i \lambda_i\lvert_p \\&= \lambda_j\lvert_p ,\end{align}

where \(\delta^j_i\) is the Kronecker delta defined such that \(\delta^j_i = 1\) when \(i=j\) and \(\delta^j_i = 0\) otherwise.

Thus, for each smooth function \(f\), the differential \(df_p\) can be written in coordinates as

\[df_p\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)dx^i\lvert_p = \frac{\partial f}{\partial x^i}(p)dx^i\lvert_p.\]

Cotangent Space

The cotangent space \(T^*_pM\) at a point \(p \in M\) on a smooth manifold \(M\) is the vector space dual to the tangent space \(T_pM\), i.e. the set of linear functionals \(\omega : T_pM \rightarrow \mathbb{R}\). Given smooth coordinates \((x^i)\), the differentials \(dx^i\rvert_p\) comprise a basis for \(T^*_pM\) called the dual coordinate basis.

Pullback in Coordinates

We can examine the action of the pullback \(dF^*_p\) of a smooth map \(F : \mathbb{R}^n \rightarrow \mathbb{R}^m\) between smooth manifolds \(M\) and \(N\) relative to coordinate functions \((x^i)\) on \(\mathbb{R}^n\) and \(y^j\) on \(\mathbb{R}^m\) as follows:

\begin{align}dF^*_p\left(\omega_j dy^j\lvert_{F(p)}\right) &= dF^*_p\left(\omega_j dy^j\lvert_{F(p)}\right)\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)dx^i\lvert_p \\&=\omega_j dy^j\lvert_{F(p)}\left(dF_p\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)\right)dx^i\lvert_p \\&= \omega_j dF_p\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)(y^j)dx^i\lvert_p \\&= \omega_j \frac{\partial}{\partial x^i}\bigg\rvert_p (y^j \circ F) dx^i\lvert_p \\&= \omega_j \frac{\partial F^j}{\partial x^i}(p)dx^i\lvert_p.\end{align}

Thus, the matrix representation of this map is the \(n \times m\) matrix

\[\begin{bmatrix}\frac{\partial F^1}{\partial x^1}(p) & \dots & \frac{\partial F^m}{\partial x^1}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^1}{\partial x^n}(p) & \dots & \frac{\partial F^m}{\partial x^n}(p)\end{bmatrix},\]

since

\[\begin{bmatrix}\frac{\partial F^1}{\partial x^1}(p) & \dots & \frac{\partial F^m}{\partial x^1}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^1}{\partial x^n}(p) & \dots & \frac{\partial F^m}{\partial x^n}(p)\end{bmatrix}\begin{bmatrix}\omega_1 \\ \vdots \\ \omega_m\end{bmatrix} = \begin{bmatrix}\omega_i \frac{\partial F^i}{\partial x^1} \\ \vdots \\ \omega_i \frac{\partial F^i}{\partial x^n}.\end{bmatrix}\]

Note that this matrix is the transpose of the Jacobian matrix, i.e.

\[(DF)^T_{ij} = \frac{\partial F^j}{\partial x^i}(p) = (DF)_{ji}.\]

This implies, by properties of matrix multiplication, that \(D(G \circ F)^T = (DF)^T(DG)^T\), which we now confirm explicitly. The dual chain rule implies, for smooth maps \(F : \mathbb{R}^n \rightarrow \mathbb{R}^m\) and \(G : \mathbb{R}^m \rightarrow \mathbb{R}^l\), that the matrix which represents the pullback \(d(G \circ F)^*_p\) is the \(n \times l\) matrix \(D(G \circ F)^T = (DF)^T(DG)^T\), so that

\begin{align}D(G \circ F)^T &= \begin{bmatrix}\frac{\partial F^1}{\partial x^1}(p) & \dots & \frac{\partial F^m}{\partial x^1}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^1}{\partial x^n}(p) & \dots & \frac{\partial F^m}{\partial x^n}(p)\end{bmatrix}\begin{bmatrix}\frac{\partial G^1}{\partial y^1}(F(p)) & \dots & \frac{\partial G^l}{\partial y^1}(F(p)) \\ \vdots & \ddots & \vdots \\ \frac{\partial G^1}{\partial y^m}(F(p)) & \dots & \frac{\partial G^l}{\partial y^m}(F(p))\end{bmatrix} \\&= \begin{bmatrix}\frac{\partial F^k}{\partial x^1}(p)\frac{\partial G^1}{\partial y^k}(F(p)) & \dots & \frac{\partial F^k}{\partial x^1}(p)\frac{\partial G^l}{\partial y^k}(F(p)) \\ \vdots & \ddots & \vdots \\ \frac{\partial F^k}{\partial x^n}(p)\frac{\partial G^l}{\partial y^k}(F(p)) & \dots & \frac{\partial F^k}{\partial x^n}(p)\frac{\partial G^l}{\partial y^k}(F(p))\end{bmatrix}.\end{align}

Thus, for row \(i\) and column \(j\),

\[D(G \circ F)^T_{ij} = \left(\frac{\partial F^k}{\partial x^i}(p)\frac{\partial G^j}{\partial y^k}(F(p))\right).\]

This can be confirmed by direct calculation using the dual chain rule:

\begin{align}d(G \circ F)^*_p\left(dz^j\lvert_{G(F(p))}\right) &= dF^*_p\left(dG^*_{F(p)}\left(dz^j\lvert_{G(F(p))}\right)\right) \\&= dF^*_p\left(dG^*_{F(p)}\left(dz^j\lvert_{G(F(p))}\right)\left(\frac{\partial}{\partial y^k}\bigg\lvert_p\right) dy^k\lvert_{F(p)}\right)\\&= dF^*_p\left(dz^j\lvert_{G(F(p))}\left(dG_{F(p)}\left(\frac{\partial}{\partial y^k}\bigg\lvert_{F(p)}\right)\right)dy^k\lvert_{F(p)}\right) \\&= dF^*_p\left(dG_{F(p)}\left(\frac{\partial}{\partial y^k}\bigg\lvert_{F(p)}\right)(z^j)dy^k\lvert_{F(p)}\right) \\&= dF^*_p\left(\frac{\partial}{\partial y^k}\bigg\lvert_{F(p)}(y^j \circ G)dy^k\lvert_{F(p)}\right) \\&= dF^*_p\left(\frac{\partial}{\partial y^k}\bigg\lvert_{F(p)}(G^j)dy^k\lvert_{F(p)}\right) \\&= dF^*_p\left(\frac{\partial G^j}{\partial y^k}(F(p))dy^k\lvert_{F(p)}\right) \\&= \frac{\partial G^j}{\partial y^k}(F(p))dF^*_p\left(dy^k\lvert_{F(p)}\right) \\&= \frac{\partial G^j}{\partial y^k}(F(p))dF^*_p\left(dy^k\lvert_{F(p)}\right)\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)dx^i\lvert_p \\&= \frac{\partial G^j}{\partial y^k}(F(p))dy^k\lvert_{F(p)}\left(dF_p\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)\right)dx^i\lvert_p \\&= \frac{\partial G^j}{\partial y^k}(F(p)) dF_p\left(\frac{\partial}{\partial x^i}\bigg\rvert_p\right)(y^k)dx^i\lvert_p \\&= \frac{\partial G^j}{\partial y^k}(F(p)) \frac{\partial}{\partial x^i}\bigg\rvert_p (y^k \circ F) dx^i\lvert_p \\&=\frac{\partial G^j}{\partial y^k}(F(p)) \frac{\partial F^k}{\partial x^i}(p)dx^i\lvert_p \end{align}

Computational Graphs

The previous section indicated how total derivatives can be represented in coordinates as matrices of partial derivatives. However, computations in computer programs do not usually arise as rectangular arrays, but rather as graphs. Our goal in this section is to describe the relationship between these two formats. Consider the following expression:

\[F(x^1, x^2) = \sin x^1 + x^1x^2 + x^1.\]

This can be represented by the following computational graph:

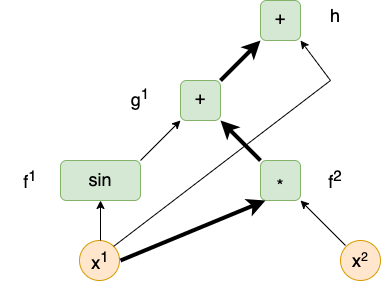
A single path from a source (representing an input parameter to the main program) to a sink (representing a component of the output of the main program) is highlighted in bold in the diagram.

The function \(F = h \circ g \circ f\) is a composite of three functions defined as follows:

• \(f(x^1, x^2) = (\sin x^1, x^1x^2, x^1)\),
• \(g(y^1, y^2, y^3) = (y^1 + y^2, y^3)\),
• \(h(z^1, z^2) = z^1 + z^2\).

The product of Jacobian matrices representing the derivative of this composite map is as follows:

\[(DF)_p = \begin{bmatrix}\frac{\partial h}{\partial z^1} & \frac{\partial h}{\partial z^2}\end{bmatrix}_{g(f(p))} \begin{bmatrix}\frac{\partial g^1}{\partial y^1} & \frac{\partial g^1}{\partial y^2} & \frac{\partial g^1}{\partial y^3} \\ \frac{\partial g^2}{\partial y^1} & \frac{\partial g^2}{\partial y^2} & \frac{\partial g^2}{\partial y^3}\end{bmatrix}_{f(p)} \begin{bmatrix}\frac{\partial f^1}{\partial x^1} & \frac{\partial f^1}{\partial x^2} \\ \frac{\partial f^2}{\partial x^1} & \frac{\partial f^2}{\partial x^2} \\ \frac{\partial f^3}{\partial x^1} & \frac{\partial f^3}{\partial x^2} \end{bmatrix}_p.\]

Observe that, when multiplying these matrices, every entry within the resultant matrix is a sum of products of partial derivatives, where each product contains exactly one partial derivative of each respective function \(h\), \(g\), \(f\). Furthermore, observe that each such product represents a path within the computational graph. For instance, the following product represents the path highlighted in bold in the figure above:

\[\frac{\partial h}{\partial z^1}(g(f(p)))\frac{\partial g^1}{\partial y^2}(f(p))\frac{\partial f^2}{\partial x^1}(p).\]

Finally, observe that the entry in which each sum of products accumulates in the final matrix is related to the respective component function (e.g. \(F^1\)) and variable (e.g. \(x^1\)).

This suggests an approach to computing derivatives using graphs: start a a source of the graph (representing an input variable), and trace all paths recursively to sinks (representing an output component). While tracing each path, accumulate the partial derivatives representing the path as a product. Once a sink is reached, accumulate the resultant product as a sum, storing it in a vector or map which associates the accumulated sum of products with the respective source variable that originated the path.

Because this process corresponds to performing a right-associative product of the respective Jacobian matrices (yet with the individual arithmetic operations in a different order) such that the operation on any vector is represented as \((DF)v\), it is often referred to as a Jacobian-vector product (JVP), and it sometimes compared to the pushforward operation (since \((DF)v\) represents the pushforward of \(v\) in coordinates).

The algorithm can also proceed starting from a sink and tracing toward each source. Consider the product of Jacobian transpose matrices from the example above:

\[(DF)^T_p = \begin{bmatrix}\frac{\partial f^1}{\partial x^1} & \frac{\partial f^2}{\partial x^1} & \frac{\partial f^3}{\partial x^1} \\ \frac{\partial f^1}{\partial x^2} & \frac{\partial f^2}{\partial x^2} & \frac{\partial f^3}{\partial x^2}\end{bmatrix}_p\begin{bmatrix}\frac{\partial g^1}{\partial y^1} & \frac{\partial g^2}{\partial y^1} \\ \frac{\partial g^1}{\partial y^2} & \frac{\partial g^2}{\partial y^2} \\ \frac{\partial g^1}{\partial y^3} & \frac{\partial g^2}{\partial y^3}\end{bmatrix}_{f(p)}\begin{bmatrix}\frac{\partial h}{\partial z^1} \\ \frac{\partial h}{\partial z^2}\end{bmatrix}_{g(f(p))}.\]

The same observations apply: each entry in the resultant matrix is the sum of products of partial derivatives, where each product represents a path within the graph. However, the products will be computed in the reverse order.

This suggests an alternative approach to computing derivatives using graphs: start a a sink of the graph (representing an output component), and trace all inverse paths recursively to sources (representing an input variable). While tracing each inverse path, accumulate the partial derivatives representing the path as a product. Once a source is reached, accumulate the resultant product as a sum, storing it in a vector or map which associates the accumulated sum of products with the respective sink component that originated the inverse path.

Because this process corresponds to performing a right-associative product of the respective Jacobian transpose matrices, and since \((DF)^Tv = v^T(DF)\), it is often referred to as a vector-Jacobian product (VJP), and it sometimes compared to the pullback operation (since \((DF)^Tv\) represents the pullback of \(v\) in coordinates).

Automatic Differentiation

Consider the following expression:

\[\sin x^1 + x^1x^2 + x^1.\]

This is a map with signature \(\mathbb{R}^2 \rightarrow \mathbb{R}\) which is the composite \(h \circ g \circ f\) of functions \(f : \mathbb{R}^2 \rightarrow \mathbb{R}^3\), \(g : \mathbb{R}^3 \rightarrow \mathbb{R}^2\), and \(h : \mathbb{R}^2 \rightarrow \mathbb{R}\) defined as follows:

• \(f(x^1, x^2) = (\sin x^1, x^1x^2, x^1)\),
• \(g(y^1, y^2, y^3) = (y^1 + y^2, y^3)\),
• \(h(z^1, z^2) = z^1 + z^2\).

This expression can be represented as a directed acyclic graph (DAG) as follows:

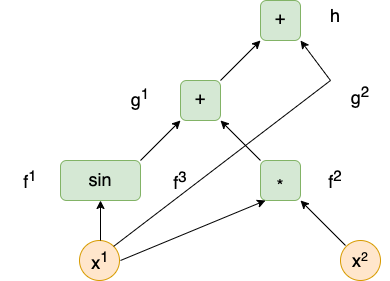
Each node represents a component function, and each component function represents an atomic operation (one that cannot be decomposed further as the composite of two or more operations). Incoming edges are ordered from left to right. The \(j\)-th incoming edge of a node corresponds to the \(j\)-th coordinate of the domain of the component function represented by the node. Each edge indicates the composition of these functions. The sources of the graph (the nodes with only outgoing edges) represent the coordinate functions (variables), and the sinks (the nodes with only incoming edges) represent the component functions of the main expression.

The Jacobian matrix representing this expression is the following product:

\[\begin{bmatrix}\frac{\partial h}{\partial z^1} & \frac{\partial h}{\partial z^2}\end{bmatrix}_{g(f(p))} \begin{bmatrix}\frac{\partial g^1}{\partial y^1} & \frac{\partial g^1}{\partial y^2} & \frac{\partial g^1}{\partial y^3} \\ \frac{\partial g^2}{\partial y^1} & \frac{\partial g^2}{\partial y^2} & \frac{\partial g^2}{\partial y^3}\end{bmatrix}_{f(p)} \begin{bmatrix}\frac{\partial f^1}{\partial x^1} & \frac{\partial f^1}{\partial x^2} \\ \frac{\partial f^2}{\partial x^1} & \frac{\partial f^2}{\partial x^2} \\ \frac{\partial f^3}{\partial x^1} & \frac{\partial f^3}{\partial x^2} \end{bmatrix}_p.\]

The actual values are

\[\begin{bmatrix}1 & 1\end{bmatrix}\begin{bmatrix}1 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}0 & \cos p^1 \\ p^1 & p^2 \\ 0 & 1\end{bmatrix} = \begin{bmatrix}\cos p^1 + p^2 + 1 & p^1\end{bmatrix}.\]

Our goal is to adapt the matrix calculation (expressed in terms of rows and columns) to a graph calculation (expressed in terms of nodes and edges). Each node represents a component function (for instance, \(f^1(x^1, x^2) = \sin x^1\), and \(g^1(y^1, y^2, y^3) = y^1 + y^2\)).

The variables can be considered as coordinate functions (i.e. \(x^1(x,y)=x\) and \(x^2(x,y)=y\)) or as component functions of the identity map \(\mathrm{Id}_{\mathbb{R}^2}\). We can then consider the composite \(h \circ g \circ f \circ \mathrm{Id}_{\mathbb{R}^2}\). The Jacobian product representing this composite is

\[\begin{bmatrix}\frac{\partial h}{\partial z^1} & \frac{\partial h}{\partial z^2}\end{bmatrix}_{g(f(p))} \begin{bmatrix}\frac{\partial g^1}{\partial y^1} & \frac{\partial g^1}{\partial y^2} & \frac{\partial g^1}{\partial y^3} \\ \frac{\partial g^2}{\partial y^1} & \frac{\partial g^2}{\partial y^2} & \frac{\partial g^2}{\partial y^3}\end{bmatrix}_{f(p)} \begin{bmatrix}\frac{\partial f^1}{\partial x^1} & \frac{\partial f^1}{\partial x^2} \\ \frac{\partial f^2}{\partial x^1} & \frac{\partial f^2}{\partial x^2} \\ \frac{\partial f^3}{\partial x^1} & \frac{\partial f^3}{\partial x^2} \end{bmatrix}_p \begin{bmatrix}\frac{\partial x^1}{\partial x^1} & \frac{\partial x^1}{\partial x^2} \\ \frac{\partial x^2}{\partial x^1} & \frac{\partial x^2}{\partial x^2}\end{bmatrix}_p,\]

whose values are

\[\begin{bmatrix}1 & 1\end{bmatrix}\begin{bmatrix}1 & 1 & 0 \\ 0 & 0 & 1\end{bmatrix}\begin{bmatrix}0 & \cos p^1 \\ p^1 & p^2 \\ 0 & 1\end{bmatrix} \begin{bmatrix}1 & 0 \\ 0 & 1\end{bmatrix}= \begin{bmatrix}\cos p^1 + p^2 + 1 & p^1\end{bmatrix}.\]

Although mathematically superfluous, this allows us to consider every node in the graph as representing a component function and to treat the algorithm uniformly.

There are two approaches to automatic differentiation:

• forward accumulation - this mode begins at the sources of the graph and propagates derivatives forward (in the direction of the edges) until they finally accumulate at the sinks of the graph. Forward accumulation proceeds one source at a time, and therefore requires one iteration per variable.
• backward accumulation (reverse accumulation) - this mode begins at the sinks of the graph and propagates derivatives backward (in the opposite direction of the edges) until they finally accumulate at the sources of the graph. Backward accumulation proceeds one sink at a time, and therefore requires one iteration per component function.

Thus, for a function with signature \(\mathbb{R}^n \rightarrow \mathbb{R}^m\), when \(n \lt m\), it will be more efficient to use forward accumulation, but when \(m \lt n\), it will be more efficient to use backward accumulation. In many cases, the function being differentiated has signature \(\mathbb{R}^n \rightarrow \mathbb{R}\) with \(n\) being very large, so backward accumulation is often the preferred mode.

The forward accumulation algorithm proceeds on a function \(F : \mathbb{R}^n \rightarrow \mathbb{R}^m\) as follows:

1. Evaluate the main function using the given input, caching the value of each subexpression at its respective node. These values will be used when computing the partial derivatives.
2. Fix a single coordinate function corresponding to a source. Begin the propagation at the node representing this coordinate function. Since the partial derivative of the coordinate function with respect to itself is \(1\), propagate the initial seed value of \(1\) forward to each successor node.
3. When a seed value is propagated to a node, compute the partial derivative of the component function corresponding to the node with respect to the coordinate function corresponding to the incoming edge at the value cached in the predecessor nodes. Compute the product of the seed and the partial derivative, and propagate this product forward to each successor node.
4. Continue this process until each sink is reached. The partial derivatives are now accumulated as sums in the respective sinks.

The backward accumulation algorithm proceeds on a function \(F : \mathbb{R}^n \rightarrow \mathbb{R}^m\) as follows:

1. Evaluate the main function using the given input, caching the value of each subexpression at its respective node. These values will be used when computing the partial derivatives.
2. Fix a single component function corresponding to a sink. Begin propagation at the node representing this component function. For each predecessor, compute the initial seed value as the partial derivative of the selected component function with respect to the coordinate function corresponding to the predecessor, and propagate this seed backward to the predecessor.
3. When a seed value is propagated to a node, for each predecessor, compute the partial derivative of the component function corresponding to the node with respect to the coordinate function corresponding to the predecessor, and propagate the product of the seed value with this partial derivative backward to the predecessor.
4. Continue this process until each source is reached. The partial derivatives accumulate as a sum at each source. The partial derivatives of the fixed component function with respect to each coordinate are now accumulated in the respective source nodes.

Example

First, consider forward accumulation using the example above:

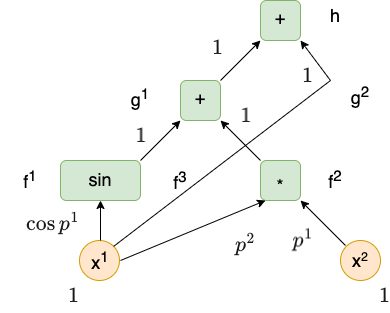
1. Select coordinate function \(x^1\).
   1. Propagate the initial seed value of \((\partial x^1/\partial x^1)(p) = 1\) to the node representing \(f^1(x^1, x^2) = \sin x^1\). Compute the partial derivative \((\partial f^1/\partial x^1)(p) = \cos p^1\).
      1. Propagate the accumulated seed value of \(1 \cdot \cos p^1\) to the node representing \(g^1(y^1,y^2,y^3) = y^1 + y^2\). Compute the partial derivative \((\partial g^1/\partial y^1)(f(p)) = 1\).
         1. Propagate the accumulated seed value of \(1 \cdot \cos p^1 \cdot 1\) to the node representing \(h(z^1,z^2) = z^1 + z^2\). Compute the partial derivative \((\partial h/\partial z^1)(g(f(p))) = 1\). Accumulate the intermediate result \(1 \cdot \cos p^1 \cdot 1 \cdot 1 = \cos p^1\).
   2. Propagate the initial seed value of \((\partial x^1/\partial x^1)(p) = 1\) to the node representing \(f^2(x^1, x^2) = x^1x^2\). Compute the partial derivative \((\partial f^2/\partial x^1)(p) = p^2\).
      1. Propagate the accumulated seed value of \(1 \cdot p^2\) to the node representing \(g^1(y^1,y^2,y^3) = y^1 + y^2\). Compute the partial derivative \((\partial g^1/\partial y^2)(f(p)) = 1\).
         1. Propagate the accumulated seed value of \(1 \cdot p^2 \cdot 1\) to the node representing \(h(z^1,z^2) = z^1 + z^2\). Compute the partial derivative \((\partial h/\partial z^1)(g(f(p))) = 1\). Accumulate the intermediate result \(1 \cdot p^2 \cdot 1 \cdot 1 = p^2\). Add this result to the existing intermediate result to obtain \(\cos p^1 + p^2\).
   3. Propagate the initial seed value of \((\partial x^1/\partial x^1)(p) = 1\) to the node representing \(h(z^1, z^2) =z^1 + z^2\). Compute the partial derivative \((\partial h/\partial z^2)(p) = 1\). Accumulate the intermediate result \(1 \cdot 1\). Add this result to the existing intermediate result to obtain \(\cos p^1 + p^2 + 1\).
2. Select coordinate function \(x^2\).
   1. Propagate the initial seed value of \((\partial x^2/\partial x^2)(p) = 1\) to the node representing \(f^2(x^1, x^2) = x^1x^2\). Compute the partial derivative \((\partial f^2/\partial x^2)(p) = p^1\).
      1. Propagate the accumulated seed value of \(1 \cdot p^1\) to the node representing \(g^1(y^1,y^2,y^3) = y^1 + y^2\). Compute the partial derivative \((\partial g^1/\partial y^2)(f(p)) = 1\).
         1. Propagate the accumulated seed value of \(1 \cdot p^1 \cdot 1\) to the node representing \(h(z^1,z^2) = z^1 + z^2\). Compute the partial derivative \((\partial h/\partial z^2)(g(f(p))) = 1\). Accumulate the intermediate result \(1 \cdot p^1 \cdot 1 \cdot 1 = p^1\).

The final result is computed to be \((\cos p^1 + p^2 + 1, p^1)\).

Next, consider backward accumulation using the same example.

1. Select the (only) component function \(h(z^1, z^2) = z^1 + z^2\).
   1. Compute the partial derivative \((\partial h/\partial z^1)(g(f(p))) = 1\). Propagate the initial seed value \(1\) to the node representing \(g^1(y^1,y^2,y^3) = y^1 + y^2\).
      1. Compute the partial derivative \((\partial g^1/\partial y^1)(f(p)) = 1\). Propagate the accumulated seed value of \(1 \cdot 1\) to the node representing \(f^1(x^1, x^2) = \sin x^1\).
         1. Compute the partial derivative \((\partial f^1/\partial x^1)(p) = \cos p^1\). Accumulate the intermediate result of \(1 \cdot 1 \cdot \cos p^1 = p^1\) to the node representing \(x^1\).
      2. Compute the partial derivative \((\partial g^1/\partial y^2)(f(p)) = 1\). Propagate the accumulated seed value of \(1 \cdot 1\) to the node representing \(f^2(x^1, x^2) = x^1x^2\).
         1. Compute the partial derivative \((\partial f^2/\partial x^1)(p) = p^2\). Add the intermediate result of \(1 \cdot 1 \cdot p^2 = p^2\) to the existing intermediate result in the node representing \(x^1\), obtaining \(\cos p^1 + p^2\).
         2. Compute the partial derivative \((\partial f^2/\partial x^2)(p) = p^1\). Add the intermediate result of \(1 \cdot 1 \cdot p^1 = p^1\) to the node representing \(x^2\), obtaining \(p^1\).
   2. Compute the partial derivative \((\partial h/\partial z^2)(g(f(p))) = 1\). Add the intermediate result of \(1\) to the node representing \(x^1\), obtaining \(\cos p^1 + p^2 + 1\).

The final result is computed to be \((\cos p^1 + p^2 + 1, p^1)\). However, note that only one graph traversal was necessary.

Example

Consider the example of spherical coordinates (on the unit sphere):

\[(\sin \theta \cos \varphi, \sin \theta \sin \varphi, \cos \theta).\]

This is the composition \(g \circ f\) of the following functions:

• \(f(\theta, \varphi) = (\sin \theta, \cos \varphi, \sin \varphi, \cos \theta)\),
• \(g(y^1,y^2,y^3,y^4) = (y^1y^2, y^1y^3, y^4)\).

The directed acyclic graph (DAG) representing this expression is depicted in Figure 2.

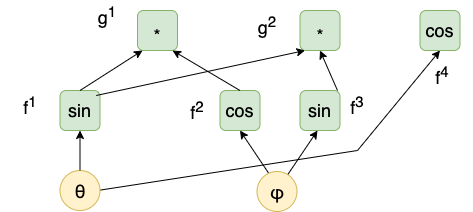
The forward accumulation algorithm proceeds as follows:

1. Select coordinate function \(\theta\).
   1. Propagate the initial seed value of \((\partial \theta/\partial \theta)(p) = 1\) to the node representing \(f^1(\theta, \varphi) = \sin \theta\). Compute the partial derivative \((\partial f^1/\partial \theta)(p) = \cos p^1\).
      1. Propagate the accumulated seed value of \(1 \cdot \cos p^1\) to the node representing \(g^1(y^1,y^2,y^3,y^4) = y^1y^2\). Compute the partial derivative \((\partial g^1/\partial y^1)(f(p)) = \cos p^2\). Accumulate the intermediate result \(1 \cdot \cos p^1 \cdot \cos p^2 = \cos p^1 \cdot \cos p^2\).
      2. Propagate the accumulated seed value of \(1 \cdot \cos p^1\) to the node representing \(g^2(y^1,y^2,y^3,y^4) = y^1y^3\). Compute the partial derivative \((\partial g^2/\partial y^1)(f(p)) = \sin p^2\). Accumulate the intermediate result \(1 \cdot \cos p^1 \cdot \sin p^2 = \cos p^1 \cdot \sin p^2\).
   2. Propagate the initial seed value of \((\partial \theta/\partial \theta)(p) = 1\) to the node representing \(f^4(\theta, \varphi) = \cos \theta\). Compute the partial derivative \((\partial f^4/\partial \theta)(p) = -\sin p^1\). Accumulate the intermediate result \(1 \cdot -\sin p^1 = -\sin p^1\).
2. Select coordinate function \(\varphi\).
   1. Propagate the initial seed value of \((\partial \varphi/\partial \varphi)(p) = 1\) to the node representing \(f^2(\theta, \varphi) = \cos \varphi\). Compute the partial derivative \((\partial f^2/\partial \varphi)(p) = -\sin p^2\).
      1. Propagate the accumulated seed value of \(1 \cdot -\sin p^2\) to the node representing \(g^1(y^1,y^2,y^3,y^4) = y^1y^2\). Compute the partial derivative \((\partial g^1/\partial y^2)(f(p)) = \sin p^1\). Accumulate the intermediate result \(1 \cdot -\sin p^2 \cdot \sin p^1 = -\sin p^2 \cdot \sin p^1\).
   2. Propagate the initial seed value of \((\partial \varphi/\partial \varphi)(p) = 1\) to the node representing \(f^3(\theta, \varphi) = \sin \varphi\). Compute the partial derivative \((\partial f^3/\partial \varphi)(p) = \cos p^2\).
      1. Propagate the accumulated seed value of \(1 \cdot \cos p^2\) to the node representing \(g^2(y^1,y^2,y^3,y^4) = y^1y^3\). Compute the partial derivative \((\partial g^2/\partial y^3)(f(p)) = \sin p^1\). Accumulate the intermediate result \(1 \cdot \cos p^2 \cdot \sin p^1 = \cos p^2 \cdot \sin p^1\).

The final result is

\[\begin{bmatrix}\cos p^1 \cos p^2 & -\sin p^1\sin p^2 \\ \cos p^1 \sin p^2 & \sin p^1 \cos p^2 \\ -\sin p^1 & 0\end{bmatrix}.\]

The backward accumulation proceeds as follows:

1. Select component function \(g^1(y^1,y^2,y^3,y^4) = y^1y^2\).
   1. Compute the partial derivative \((\partial g^1/\partial y^1)(f(p)) = \cos p^2\). Propagate the initial seed value of \(\cos p^2\) to the node representing \(f^1\).
      1. Compute the partial derivative \((\partial f^1/\partial \theta)(p) = \cos p^1\). Accumulate the intermediate result \(\cos p^2 \cdot \cos p^1\).
   2. Compute the partial derivative \((\partial g^1/\partial y^2)(f(p)) = \sin p^1\). Propagate the initial seed value of \(\cos p^2\) to the node representing \(f^2\).
      1. Compute the partial derivative \((\partial f^2/\partial \varphi)(p) = -\sin p^1\). Accumulate the intermediate result \(\sin p^1 \cdot -\sin p^1\).
2. Select component function \(g^2(y^1,y^2,y^3,y^4) = y^1y^3\).
   1. Compute the partial derivative \((\partial g^2/\partial y^1)(f(p)) = \sin p^2\). Propagate the initial seed value of \(\sin p^2\) to the node representing \(f^1\).
      1. Compute the partial derivative \((\partial f^1/\partial \theta)(p) = \cos p^1\). Accumulate the intermediate result \(\sin p^2 \cdot \cos p^1\).
   2. Compute the partial derivative \((\partial g^2/\partial y^3)(f(p)) = \sin p^1\). Propagate the initial seed value of \(\sin p^1\) to the node representing \(f^3\).
      1. Compute the partial derivative \((\partial f^3/\partial \varphi)(p) = \cos p^2\). Accumulate the intermediate result \(\sin p^1 \cdot\cos p^2\).
3. Select component function \(g^3 = \cos \theta\).
   1. Compute the partial derivative \((\partial g^3\partial \theta)(p) = -\sin \theta\). Accumulate the intermediate result \(-\sin \theta\).

The final result is

\[\begin{bmatrix}\cos p^1 \cos p^2 & \cos p^1 \sin p^2 & -\sin p^1 \\ -\sin p^1\sin p^2 & \sin p^1 \cos p^2 & 0\end{bmatrix}.\]

Code

The following code listing demonstrates the basic algorithm:

import math

class Node:	
	def __init__(self, id, operation, predecessors=[]):
		self.id = id
		self.operation = operation
		self.predecessors = predecessors
		self.successors = []
		self.derivatives = []
		self.values = None
		for predecessor in predecessors:
			predecessor.successors.append(self)

	def evaluate(self):
		for predecessor in self.predecessors:
			predecessor.evaluate()
		self.value = self.operation.apply(self.predecessor_values())
        
	def forward(self, accumulation_index, id=0, seed=1.0):
		derivative = self.operation.derivative(self.index(id), self.predecessor_values())
		if not self.successors:
			self.accumulate(accumulation_index, seed * derivative)
			return
		for successor in self.successors:
 			successor.forward(accumulation_index, self.id, seed * derivative)
        
	def backward(self, accumulation_index, seed=1.0):
		if not self.predecessors:
			self.accumulate(accumulation_index, seed)
			return
		for (index, predecessor) in enumerate(self.predecessors):
			derivative = self.operation.derivative(index, self.predecessor_values())
			predecessor.backward(accumulation_index, seed * derivative)
            
	def accumulate(self, index, derivative):
		if len(self.derivatives) <= index:
			self.derivatives.extend([0.0] * (index - len(self.derivatives) + 1))
		self.derivatives[index] += derivative
        
	def index(self, id):
		return next((index for index, node in enumerate(self.predecessors) if node.id == id), 0)
        
	def predecessor_values(self):
		return list(map(lambda node: node.value, self.predecessors))
        
class Op:
	def apply(self, values):
		pass
	def derivative(self, index):
		pass
        
class Mul(Op):
	def apply(self, values):
		return values[0] * values[1]
	def derivative(self, index, values):
		if index == 0:
			return values[1]
		elif index == 1:
			return values[0]
        
class Add(Op):
	def apply(self, values):
		return values[0] + values[1]
	def derivative(self, index, values):
		return 1.0
        
class Sin(Op):
	def apply(self, values):
		return math.sin(values[0])
	def derivative(self, index, values):
		return math.cos(values[0])

class Cos(Op):
	def apply(self, values):
		return math.cos(values[0])
	def derivative(self, index, values):
		return -math.sin(values[0])
        
class Var(Op):
	def __init__(self, value):
		self.value = value
	def apply(self, values):
		return self.value
	def derivative(self, index, values):
		return 1.0

We can compute the result of the first example as follows:

n1 = Node(1, Var(2.0))
n2 = Node(2, Var(3.0))
n3 = Node(3, Sin(), [n1])
n4 = Node(4, Mul(), [n1, n2])
n5 = Node(5, Add(), [n3, n4])
n6 = Node(6, Add(), [n5, n1])

n6.evaluate()
print(n6.value)
n6.backward(0)
print(n1.derivatives)
print(n2.derivatives)
n1.forward(0)
n2.forward(1)
print(n6.derivatives)

This yields the following result:

8.909297426825681
[3.5838531634528574]
[2.0]
[3.5838531634528574, 2.0]

We can compute the result of the second example as follows:

n1 = Node(1, Var(2.0))
n2 = Node(2, Var(3.0))
n3 = Node(3, Sin(), [n1])
n4 = Node(4, Cos(), [n2])
n5 = Node(5, Sin(), [n2])
n6 = Node(6, Cos(), [n1])
n7 = Node(7, Mul(), [n3, n4])
n8 = Node(8, Mul(), [n3, n5])

n6.evaluate()
n7.evaluate()
n8.evaluate()
print("(" + str(n6.value) + ", " + str(n7.value) + ", " + str(n8.value) + ")")
n6.backward(0)
n7.backward(1)
n8.backward(2)
print(n1.derivatives)
print(n2.derivatives)
n1.forward(0)
n2.forward(1)
print(n6.derivatives)
print(n7.derivatives)
print(n8.derivatives)

This yields the following result:

(-0.4161468365471424, -0.9001976297355174, 0.12832006020245673)
[-0.9092974268256817, 0.411982245665683, -0.05872664492762098]
[0.0, -0.12832006020245673, -0.9001976297355174]
[-0.9092974268256817]
[0.411982245665683, -0.12832006020245673]
[-0.05872664492762098, -0.9001976297355174]

In the example program, the computational graph was constructed explicitly. In practice, there are many ways to construct such graphs, but one common method exploits operator overloading in programming languages that support it (such as Python). In this manner, graphs can be constructed using ordinary operators within the programming language. For instance, we could augment the previous code listing as follows:

class Node:
	counter = 0

    ...
        
	def __add__(self, other):
		return Node(Node.next_id(), Add(), [self, other])
        
	def __mul__(self, other):
		return Node(Node.next_id(), Mul(), [self, other])
        
	@staticmethod
	def next_id():
		i = Node.counter
		Node.counter = Node.counter + 1
		return i
    
def val(value):
	return Node(Node.next_id(), Var(value))
    
def sin(n):
	return Node(Node.next_id(), Sin(), [n])
    
def cos(n):
	return Node(Node.next_id(), Cos(), [n])

Then, we can construct computational graphs as follows:

v1 = val(2.0)
v2 = val(3.0)
v = sin(v1) + v1*v2 + v1
v.evaluate()
v.backward(0)
print(v.value)
print(v1.derivatives)
print(v2.derivatives)

This yields the same result:

8.909297426825681
[3.5838531634528574]
[2.0]

There are several technical issues involved with automatic differentiation. For instance, it is essential to ensure that the computational graphs represent differentiable functions. It is very easy to introduce functions that are not differentiable (and indeed are not even continuous) when conditional logic (such as "if" statements) are introduced. In this post, we are only considering the basic theory of automatic differentiation, however.