Smooth Manifolds

A manifold is a set whose elements (thought of as points) are endowed with coordinates (tuples of numbers).

Spherical Coordinates

Let's begin by considering the familiar example of the unit sphere \(S^2\). The unit sphere can be defined as an implicit surface (i.e. as the set of solutions to an equation) as follows:

\[S^2 = \{p \in \mathbb{R}^3 : \lVert p \rVert = 1\},\]

where \(\lVert p \rVert = \lVert (x,y,z) \rVert = \sqrt{x^2 + y^2 + z^2}\) is the norm (length) of the vector \(p = (x,y,z)\).

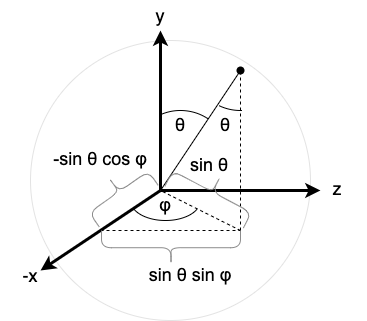
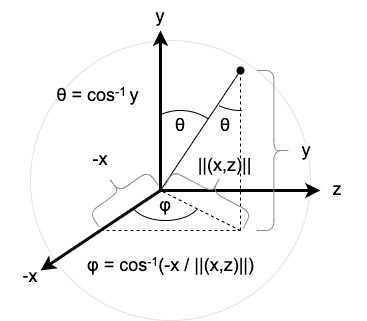
Suppose that we wish to assign coordinates to each point on the sphere. The most common method of doing so involves spherical coordinates, as depicted in Figure 1.

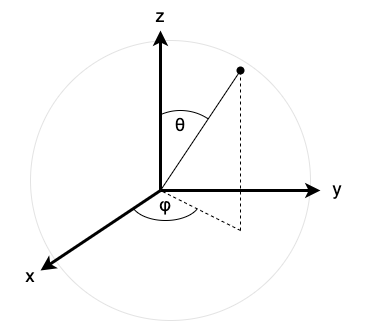
A particular axis (the "z" axis) is designated as the polar axis. An angle \(\theta\), called the polar angle, indicates the declination of the radial line (the line extending from the center of the sphere to a point on the surface of the sphere) away from the polar axis, and an angle \(\varphi\), called the azimuthal angle, indicates the rotation of the radial line about the polar axis. This is very similar to geographical coordinates specified using latitude and longitude (although the angular conventions are different, namely, longitude is the inclination above or declination below the equator, not the declination below the north pole). Together, these angles can specify any point on the sphere.

Thus, only \(2\) numbers are needed to locate each point on the sphere, and it is in this sense that the sphere is a \(2\)-dimensional geometric figure (which is embedded in the \(3\)-dimensional space \(\mathbb{R}^3\)).

The specific mapping from spherical coordinates to Cartesian coordinates is as follows:

\[(\theta, \varphi) \mapsto (\sin \theta \cos \varphi, \sin \theta \sin \varphi, \cos \theta).\]

This is also written in terms of component functions (designated as \(x\), \(y\), and \(z\)) as follows:

• \(x(\theta, \varphi) = \sin \theta \cos \varphi\),
• \(y(\theta, \varphi) = \sin \theta \sin \varphi\),
• \(z(\theta, \varphi) = \cos \theta\).

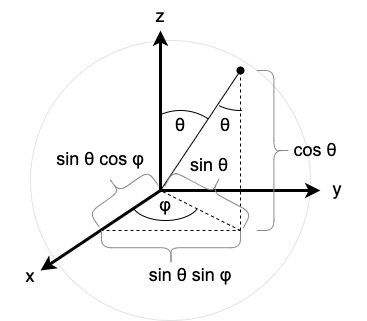
Consider Figure 2. The orthogonal projection of the radial line onto the \(xy\)-plane is the leg of a right triangle which is opposite \(\theta\), so the projection has length \(\sin \theta\). The projection forms the hypotenuse of another right triangle whose legs represent the coordinates in the \(xy\)-plane and have length \(\sin \theta \cos \varphi\) and \(\sin \theta \sin \varphi\). The orthogonal projection of the radial line onto the \(z\)-axis is \(\cos \theta\).

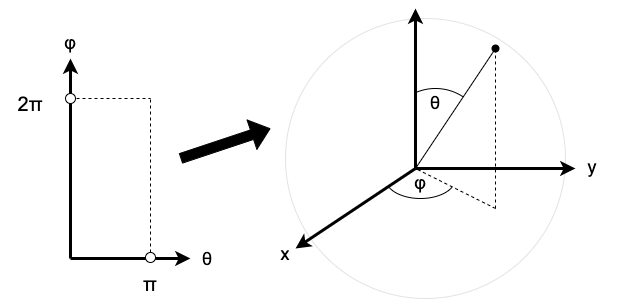
For any angles \(\theta\) and \(\varphi\), the coordinates \((\theta + 2\pi, \varphi)\) designate the same point on the sphere as the coordinates \((\theta, \varphi)\), and the coordinates \((\theta, \varphi + 2\pi)\) designate the same point on the sphere as the coordinates \((\theta, \varphi)\) (i.e. they wind a full circle around the sphere and return to the same point). Furthermore, whenever \(\theta = 0\), the coordinates \((0, \varphi)\) specify the same point, namely, the north pole, for all angles \(\varphi\), and likewise whenever \(\theta = \pi\), the coordinates \((\pi, \varphi)\) specify the same point, namely, the south pole, for all angles \(\varphi\). Thus, the domain of this mapping must be restricted (and in particular, we intend to restrict it to an open set in \(\mathbb{R}^2\) since this will allow us to induce a topology on the sphere from the topology on \(\mathbb{R}^2\)). Thus, we restrict the domain to the following open set:

\[(0, \pi) \times (0, 2\pi).\]

Defined on this domain, the mapping is injective (no two distinct coordinates map to the same point on the sphere).

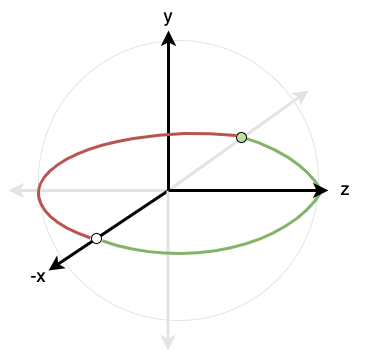
However, our actual intention is to assign coordinates to points, and not to assign points to coordinates, so we want to calculate the inverse of this mapping. Consider Figure 3.

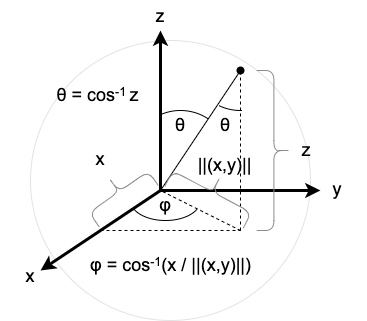
Suppose we are given a point \((x,y,z)\) on the surface of the sphere. We proceed analogously to the derivation of spherical coordinates. The orthogonal projection of the radial line onto the \(xy\)-plane is the vector \((x,y)\) (in \(\mathbb{R}^2\)) which has length \(\lVert (x,y) \rVert = \sqrt{x^2 + y^2}\). This projection forms the hypotenuse of a right triangle lying in the \(xy\)-plane which has a leg of length \(x\) adjacent to the azimuthal angle \(\varphi\)). Thus, \(\cos \varphi = x / \lVert (x,y) \rVert\) and so \(\varphi = \cos^{-1}\left(x / \lVert (x,y) \rVert\right)\). Likewise, the orthogonal projection of the radial line onto the \(z\)-axis has length \(\cos z\), and since the \(z\) component represents the leg adjacent to \(\theta\) in the corresponding right triangle, \(\theta = \cos^{-1} z\).

Now, the inverse cosine function has domain \(\cos^{-1} : (-1, 1) \rightarrow (0, \pi)\), so the expression \(\cos^{-1}\left(x / \lVert (x,y) \rVert\right)\) only defines the inverse mapping for the right hemisphere, where \(y \gt 0\) (and we also include the points where \(y=0\) and \(x \lt 0\)). The expression \(\pi + \cos^{-1}\left(-x / \lVert (x,y) \rVert\right)\) will define the inverse mapping for the left hemisphere, as in Figure 4. Since the points \(\varphi = 0\) and \(\varphi = 2\pi\) are excluded from the codomain of this mapping, so are all points where \(y = 0\) and \(x \ge 0\).

Thus, the mapping from Cartesian coordinates on the surface of the sphere to spherical coordinates is defined as follows:

\[(x,y,z) \mapsto \begin{cases}\left(\cos^{-1} z, \cos^{-1}\left(\frac{x}{\sqrt{x^2 + y^2}}\right)\right) & \text{if}~y \gt 0~\text{or if}~y = 0 ~\text{and}~x \lt 0 \\ \left(\cos^{-1} z, \pi + \cos^{-1}\left(\frac{-x}{\sqrt{x^2 + y^2}}\right)\right) & \text{if}~y \lt 0.\end{cases}\]

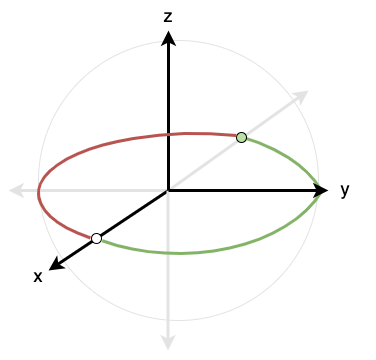
Note that the domain of this mapping is not the entire sphere, but excludes a "slit" consisting of those points where \(y = 0\) and \(x \ge 0\), as in Figure 5.

Next, suppose that \(\varphi \in (0, \pi)\). Then, for any \(\theta \in (0, \pi)\), \(y(\theta, \varphi) = \sin \theta \sin \varphi \gt 0\) since \(\sin \theta \gt 0\) and \(\sin \varphi \gt 0\). Thus, we compute

\begin{align}\varphi\left(x(\theta, \varphi), y(\theta, \varphi), z(\theta, \varphi)\right) &= \cos^{-1}\left(\frac{\sin \theta \cos \varphi}{\sqrt{(\sin \theta \cos \varphi)^2 + (\sin \theta \sin \varphi)^2}}\right) \\&= \cos^{-1}\left(\frac{\sin \theta \cos \varphi}{\sqrt{(\sin^2 \theta (\cos^2 \varphi + \sin^2 \varphi)}}\right) \\&= \cos^{-1}\left(\frac{\sin \theta \cos \varphi}{\sqrt{\sin^2 \theta}}\right) \\&= \cos^{-1}\left(\frac{\sin \theta \cos \varphi}{\lvert \sin \theta \rvert}\right) \\&= \cos^{-1}(\cos \varphi) \\&= \varphi.\end{align}

This calculation exploited the fact that \(\lvert \sin \varphi \rvert = \sin \varphi\) and \(\cos^{-1}(\cos \varphi) = \varphi\) whenever \(\varphi \in (0, \pi)\).

Now, if \(\varphi = \pi\), then \(y(\theta, \varphi) = \sin \theta \sin \varphi = 0\) and \(x(\theta, \varphi) = \sin \theta \cos \varphi \lt 0\) since \(\sin \theta \gt 0\) and \(\cos \varphi = -1\). It is still the case that \(\lvert \sin \varphi \rvert = \sin \varphi\) and \(\cos^{-1}(\cos \varphi) = \varphi\), so the prior calculation is still correct.

If \(\varphi \in (\pi, 2\pi)\), then \(\cos(\varphi) = -\cos(\varphi - \pi)\), and \(y(\theta, \varphi) = \sin \theta \sin \varphi \lt 0\) since \(\sin \theta \gt 0\) and \(\sin \varphi \lt 0\), and thus

\begin{align}\varphi\left(x(\theta, \varphi), y(\theta, \varphi), z(\theta, \varphi)\right) &= \pi + \cos^{-1}\left(\frac{-\sin \theta \cos \varphi}{\sqrt{(\sin \theta \cos \varphi)^2 + (\sin \theta \sin \varphi)^2}}\right) \\&= \pi + \cos^{-1}\left(\frac{-\sin \theta \cos \varphi}{\sqrt{(\sin^2 \theta (\cos^2 \varphi + \sin^2 \varphi)}}\right) \\&= \pi + \cos^{-1}\left(\frac{-\sin \theta \cos \varphi}{\sqrt{\sin^2 \theta}}\right) \\&= \pi + \cos^{-1}\left(\frac{-\sin \theta \cos \varphi}{\lvert \sin \theta \rvert}\right) \\&= \pi + \cos^{-1}(-\cos \varphi) \\&= \pi + \cos^{-1}(\cos (\varphi - \pi)) \\&= \pi + (\varphi - \pi) \\&= \varphi.\end{align}

Since \(\theta \in (0, \pi)\), \(\theta(x(\theta, \varphi), y(\theta, \varphi)), z(\theta, \varphi) = \cos(\cos^{-1} \theta) = \theta\).

Thus, these equations hold for \(\varphi \in (0, \pi) \cup [\pi, \pi] \cup (\pi, 2\pi) = (0, 2\pi)\) and for \(\theta \in (0, \pi)\), and hence for the entire domain \((0, \pi) \times (0, 2\pi)\).

Next, suppose \(y \gt 0\) or \(y = 0\) and \(x \lt 0\). Then we compute

\begin{align}x(\theta(x, y, z), \varphi(x,y,z)) &= \sin(\cos^{-1} z) \cos\left(\cos^{-1}\left(\frac{x}{\sqrt{x^2+y^2}}\right)\right) \\&= \sin(\cos^{-1} z) \left(\frac{x}{\sqrt{x^2+y^2}}\right) \\&= \sqrt{1 - z^2}\left(\frac{x}{\sqrt{x^2+y^2}}\right) \\&= x.\end{align}

This calculation used the Pythagorean Theorem, namely, \(\sin^2 \theta + \cos^2 \theta = 1\), and thus \(\sin \theta = \sqrt{1 - \cos^2 \theta}\) and \(\sin(\cos^{-1} z) = \sqrt{1 - \cos^2(\cos^{-1} z)} = \sqrt{1 - z^2}\). Furthermore, since \(x^2 + y^2 + z^2 = 1\), it follows that \(1 - z^2 = x^2 + y^2\).

Now, suppose that \(y \lt 0\). We compute

\begin{align}y(\theta(x, y, z), \varphi(x,y,z)) &= \sin(\cos^{-1} z) \sin\left(\pi + \cos^{-1}\left(\frac{-x}{\sqrt{x^2+y^2}}\right)\right) \\&= \sin(\cos^{-1} z) \left(-\sin\left(\cos^{-1}\left(\frac{-x}{\sqrt{x^2+y^2}}\right)\right)\right) \\&= \sin(\cos^{-1} z) \left(-\sqrt{1 - \left(\frac{-x}{\sqrt{x^2+y^2}}\right)^2}\right) \\&= \sin(\cos^{-1} z) \left(-\sqrt{1 - \left(\frac{-x}{\sqrt{1-z^2}}\right)^2}\right) \\&= \sqrt{1-z^2} \left(-\sqrt{1 - \left(\frac{-x}{\sqrt{1-z^2}}\right)^2}\right) \\&= -\sqrt{(1-z^2)\left(1 - \left(\frac{-x}{\sqrt{1-z^2}}\right)^2\right)} \\&= -\sqrt{1-z^2-x^2} \\&= -\sqrt{y^2} \\&= - \lvert y \rvert \\&= y.\end{align}

Finally, we also compute

\[z(\theta(x,y,z), \varphi(x,y,z)) = \cos^{-1}(\cos z) = z.\]

These equations thus hold on the entire domain, and there is therefore a bijection between the sets:

\[S^2 \setminus \{(x,y,z) \in S^2 : y = 0 ~\text{and}~ x \ge 0\} \cong (0,\pi) \times (0,2\pi).\]

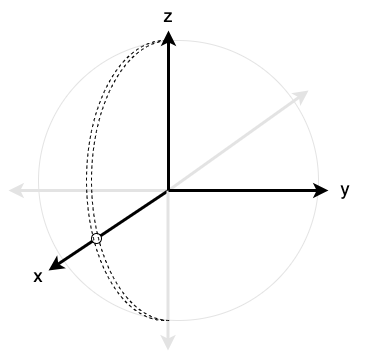
In order to cover the entire sphere, a second coordinate mapping is required. We will construct a mapping perpendicular to the previous mapping. This way, the "slits" of each respective mapping will be perpendicular, and will not overlap, so, together, the mappings will cover the entire sphere (see Figure 6).

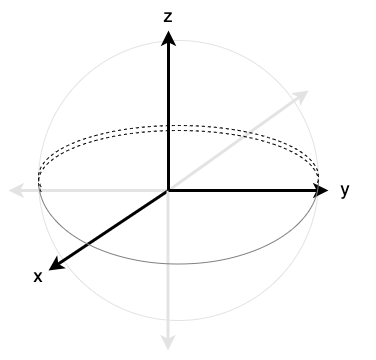
This perpendicular mapping will utilize the \(y\)-axis as the polar axis. The polar angle \(\theta\) will indicate the declination from the \(y\)-axis, and the azimuthal angle \(\varphi\) will indicate counterclockwise rotation about the \(y\)-axis. This mapping is easiest to visualize by rotating the axes such that they are oriented in a manner similar to the original diagram, as in Figure 7.

This mapping is defined as follows:

\[(\theta, \varphi) \mapsto (-\sin \theta \cos \varphi, \cos \theta, \sin \theta \sin \varphi).\]

In terms of component functions, this mapping is:

• \(x(\theta, \varphi) = -\sin \theta \cos \varphi\),
• \(y(\theta, \varphi) = \cos \theta\),
• \(z(\theta, \varphi) = \sin \theta \sin \varphi\).

The inverse mapping for perpendicular spherical coordinates is defined analogously to the inverse mapping for spherical coordinates, as in Figure 8.

We likewise define the domain of the inverse mapping for perpendicular spherical coordinates in a manner analogous to how we previously defined the domain of the inverse mapping for spherical coordinates, as in Figure 9.

Thus, the mapping from Cartesian coordinates on the surface of the sphere to spherical coordinates is defined as follows:

\[(x,y,z) \mapsto \begin{cases}\left(\cos^{-1} y, \cos^{-1}\left(\frac{-x}{\sqrt{x^2 + z^2}}\right)\right) & \text{if}~z \gt 0~\text{or if}~z = 0 ~\text{and}~x \gt 0 \\ \left(\cos^{-1} y, \pi + \cos^{-1}\left(\frac{x}{\sqrt{x^2 + z^2}}\right)\right) & \text{if}~z \lt 0.\end{cases}\]

A calculation similar to the one above for spherical coordinates shows that the mapping from perpendicular spherical coordinates to Cartesian coordinates and the mapping from Cartesian coordinates to perpendicular spherical coordinates are indeed mutual inverses, and there is therefore a bijection between the following sets:

\[S^2 \setminus \{(x,y,z) \in S^2 : z = 0 ~\text{and}~ x \lt 0\} \cong (0,\pi) \times (0,2\pi).\]

Thus, we have two mappings which assign coordinates to the points on the sphere. When the domains of these mappings overlap, we should be able to transition from one set of coordinates to the other on the overlap, as in Figure 10.

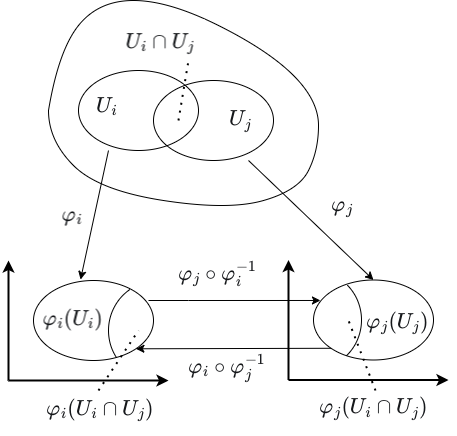
Given charts \((U_i, \varphi_i)\) and \((U_j, \varphi_j)\), the transition maps are the following maps:

• \(\varphi_j \circ \varphi_i^{-1} : \varphi_i(U_i \cap U_j) \rightarrow \varphi_j(U_i \cap U_j)\),
• \(\varphi_i \circ \varphi_j^{-1} : \varphi_j(U_i \cap U_j) \rightarrow \varphi_i(U_i \cap U_j)\).

We require these transition maps to be smooth maps. As it turns out, using the two charts from this example, both transition maps are the same; the transition map between the two charts for the sphere is given as follows:

\[(\theta, \varphi) \mapsto \begin{cases}\left(\cos^{-1}(\sin \theta \sin \varphi), \cos^{-1}\left(\frac{-\sin \theta \cos \varphi}{\sqrt{\sin^2 \theta \cos^2 \varphi + \cos^2 \theta}}\right)\right) & \text{if}~\cos \theta \gt 0 ~\text{or if}~ \cos \theta = 0 ~\text{and}~ \cos \varphi \gt 0 \\ \left(\cos^{-1}(\sin \theta \sin \varphi), \pi + \cos^{-1}\left(\frac{\sin \theta \cos \varphi}{\sqrt{\sin^2 \theta \cos^2 \varphi + \cos^2 \theta}}\right)\right)& \text{if}~ \cos \theta \lt 0.\end{cases}\]

Note that \(\sin \theta \gt 0\) since \(\theta \in (0,\pi)\) . This function is indeed smooth since it is either the composition, sum, or product of smooth functions. The conditions restrict the square root function to a non-negative domain on which it is smooth.

Stereographic Projection

Let's next consider another way to assign coordinates to the unit sphere. Consider Figure 11.

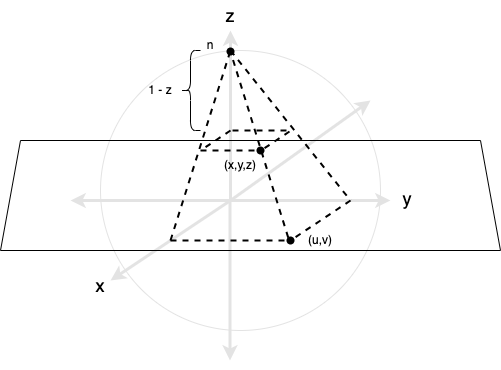
The stereographic projection of the unit sphere onto the \(xy\)-plane works as follows: first, a convenient point is chosen; we will select the north pole \(n = (0,0,1)\). For each point \((x,y,z)\) on the sphere, there exists a corresponding pair of similar triangles, one on the \(xz\)-plane, and one on the \(yz\)-plane, as depicted in the figure. This means that the following ratios are satisfied:

• \(\frac{1}{1-z} = \frac{u}{x}\),
• \(\frac{1}{1-z} = \frac{v}{y}\).

Note that these ratios are preserved even for negative values of \(z\).

Thus, the coordinates of the projection of the point \((x,y,z)\) onto the \(xy\)-plane can be computed as

\[(u,v) = \frac{1}{1-z}(x,y).\]

The codomain of this mapping is the entire plane \(\mathbb{R}^2\), which is an open set.

This will assign each point on the sphere (except for the north pole itself) unique coordinates within the \(xy\)-plane. Thus, this assigns coordinates to \(S^2 \setminus \{n\}\).

To see that this mapping is bijective, i.e. that \(S^2 \setminus \{n\} \cong \mathbb{R}^2\), note the following:

\begin{align}u^2 + v^2 &= \left(\frac{1}{1-z}x\right)^2 + \left(\frac{1}{1-z}y\right)^2 \\&= \frac{x^2+y^2}{(1-z)^2} \\&= \frac{1-z^2}{(1-z)^2}.\end{align}

The final equality is due to the fact that \(x^2+y^2+z^2=1\). We can then solve

\begin{align}\frac{1-z^2}{(1-z)^2} &= \frac{(1-z)^2 + (2z - 2z^2)}{(1-z)^2} \\&= \frac{(1-z)^2}{(1-z)^2} + \frac{2z - 2z^2}{(1-z)^2} \\&= 1 + \frac{2z(1-z)}{(1-z)^2} \\&= 1 + \frac{2z}{1-z}.\end{align}

Thus, it follows that

\[u^2 + v^2 = 1 + \frac{2z}{1-z},\]

and solving this yields

\[z = \frac{u^2 + v^2 - 1}{u^2 + v^2 + 1}.\]

Then, since \(x = u(1-z)\), we compute

\begin{align}u(1-z) &= u\left(\frac{u^2 + v^2 + 1}{u^2 + v^2 + 1} - \frac{u^2 + v^2 - 1}{u^2 + v^2 + 1}\right) \\&= \frac{2u}{u^2 + v^2 + 1}.\end{align}

Thus, the inverse mapping is

\[(u,v) \mapsto \left(\frac{2u}{u^2 + v^2 + 1}, \frac{2v}{u^2 + v^2 + 1}, \frac{u^2 + v^2 - 1}{u^2 + v^2 + 1}\right).\]

This mapping is indeed the inverse mapping of the stereographic projection, so the mapping is bijective.

In order to assign coordinates to the entire sphere, we will require a second projection. We can proceed by choosing the south pole \(s = (0,0,-1)\) and defining the mapping as

\[(u,v) = \frac{1}{1+z}(x,y).\]

Together, these two mappings cover the entire unit sphere.

The transition map from stereographic coordinates with respect to the north pole to stereographic coordinates with respect to the south pole is given by

\[(u,v) \mapsto \frac{1}{u^2 + v^2}(u,v),\]

which is a smooth function.

Smooth Manifolds

We are now ready to define smooth manifolds in general.

A chart on a set \(M\) is a pair \((U,\varphi)\) where \(U \subseteq M\) and \(\varphi\) is a bijective map from \(U\) onto an open subset \(\varphi(U) \subseteq \mathbb{R}^n\). The integer \(n\) is called the dimension of the chart.

An atlas is a collection of charts \((U_i, \varphi_i)\) on a set \(M\) such that the following properties are satisfied:

• \(\bigcup_iU_i = M,\) (i.e. the charts cover all of \(M\)),
• \(\varphi_i(U_i \cap U_j)\) is open in \(\mathbb{R}^n\) for all \(i,j\),
• Each transition map \(\varphi_j \circ \varphi_i^{-1}\) and its inverse are smooth maps.

The integer \(n\) is again called the dimension of the atlas.

Two atlases \(\mathcal{A}_1\) and \(\mathcal{A}_2\) on a set \(M\) are called compatible if \(\mathcal{A}_1 \cup \mathcal{A}_2\) is also an atlas on \(M\).

A smooth manifold is a set \(M\) together with an equivalence class \([\mathcal{A}]\) of compatible atlases of dimension \(n\), where \(n\) is the dimension of the manifold. A chart from an atlas in \([\mathcal{A}]\) is called an admissible chart, and \([\mathcal{A}]\) is called a smooth structure on \(M\).

Example 1

The unit sphere is a smooth manifold via spherical coordinates as follows:

• \(M = \{(x,y,z) \mid x^2 + y^2 + z^2 = 1\}\)
• \(U_1 = (0,\pi) \times (0, 2\pi)\)
• \(\varphi_1(x,y,z) = \begin{cases}\left(\cos^{-1} z, \cos^{-1}\left(\frac{x}{\sqrt{x^2 + y^2}}\right)\right) & \text{if}~y \gt 0~\text{or if}~y = 0 ~\text{and}~x \lt 0 \\ \left(\cos^{-1} z, \pi + \cos^{-1}\left(\frac{-x}{\sqrt{x^2 + y^2}}\right)\right) & \text{if}~y \lt 0.\end{cases}\)
• \(U_2 = (0,\pi) \times (0, 2\pi)\)
• \(\varphi_2(x,y,z) = \begin{cases}\left(\cos^{-1} y, \cos^{-1}\left(\frac{-x}{\sqrt{x^2 + z^2}}\right)\right) & \text{if}~z \gt 0~\text{or if}~z = 0 ~\text{and}~x \gt 0 \\ \left(\cos^{-1} y, \pi + \cos^{-1}\left(\frac{x}{\sqrt{x^2 + z^2}}\right)\right) & \text{if}~z \lt 0.\end{cases}\)

Example 2

The unit sphere is a smooth manifold via stereographic projection as follows:

• \(M = \{(x,y,z) \mid x^2 + y^2 + z^2 = 1\}\)
• \(U_1 = M \setminus \{(0,0,1)\}\)
• \(\varphi_1(x,y,z) = \frac{1}{1-z}(x,y)\)
• \(U_2 = M \setminus \{(0,0,-1)\}\)
• \(\varphi_2(x,y,z) = \frac{1}{1+z}(x,y)\)

Topology of Smooth Manifolds

Next, we consider how to induce a topology on a smooth manifold. We certainly want the domains of each coordinate chart to be an open set. One of the axioms of smooth manifolds requires that \(\varphi_i(U_i \cap U_j)\) be open in \(\mathbb{R}^n\) for all \(i\) and \(j\). We use this to define a topology on \(M\): a set \(U\) is open in \(M\) whenever \(\varphi_i(U \cap U_i)\) is open in \(\mathbb{R}^n\) for all coordinate charts \((U_i, \varphi_i)\).

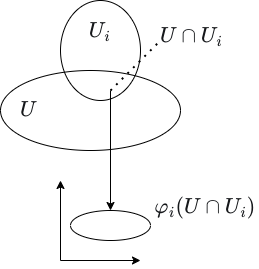
The axiom then guarantees that the domain \(U_i\) of every coordinate chart is an open set in this topology.

We need to verify that this is indeed a topology. First, observe that \(\emptyset\) is open in \(M\) since \(\varphi_i(\emptyset \cap U_i) = \emptyset\) is open in \(\mathbb{R}^n\). Next, observe that \(M\) is open in \(M\) since \(\varphi(M \cap U_i) = \varphi(U_i)\) is open in \(M\). Next, since each \(\varphi_i\) is bijective, for any open sets \(U\) and \(V\) in \(M\), it follows that

\[\varphi_i((U \cap V) \cap U_i) = \varphi_i((U \cap U_i) \cap (V \cap U_i)) =\varphi_i(U \cap U_i) \cap \varphi_i(V \cap U_i)\]

which is the intersection of open sets, and hence \(U \cap V\) is open in \(M\). Finally, for any family of open sets \(\mathcal{F}\) in \(M\),

\[\varphi_i\left(\left(\bigcup_{U \in \mathcal{F}} U \right) \cap U_i\right) = \varphi_i\left(\bigcup_{U \in \mathcal{F}} (U \cap U_i)\right) = \bigcup_{U \in \mathcal{F}}\varphi_i(U \cap U_i),\]

which is the union of open sets in \(\mathbb{R}^n\) and hence is open in \(M\).

Next, we need to verify that this topology does not depend on the choice of atlas. Suppose that \(\mathcal{A}_1\) and \(\mathcal{A}_2\) are compatible atlases for \(M\) and that a set \(U \subseteq M \) is open with respect to the topology induced by \(\mathcal{A}_1\). We want to demonstrate that \(U\) is also open with respect to the topology induced by \(\mathcal{A}_2\). Consider Figure 13.

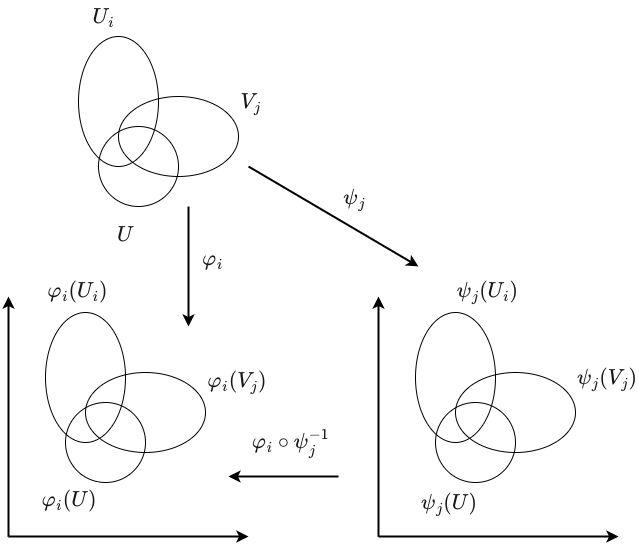
Let \(U\) be an arbitrary open set in the topology induced by \(\mathcal{A}_1\). This means that \(\varphi_i(U \cap U_i)\) is open in \(\mathbb{R}^n\) for each coordinate chart \((U_i,\varphi_i) \in \mathcal{A}_1\). Since \(\mathcal{A}_1\) and \(\mathcal{A}_2\) are compatible atlases, by definition, \(\mathcal{A}_1 \cup \mathcal{A}_2\) is an atlas, and thus \(\varphi_i(U_i \cap V_j)\) is open in \(\mathbb{R}^n\). Thus, \(\varphi_i(U \cap U_i) \cap \varphi_i(U_i \cap V_j)\) is open in \(\mathbb{R}^n\). Since \(\varphi_i\) is bijective, it follows that \(\varphi_i(U \cap U_i \cap V_j) = \varphi_i(U \cap U_i) \cap \varphi_i(U_i \cap V_j)\). Now, since \(\varphi_i(U \cap U_i \cap V_j)\) is the intersection of an open set in \(\mathbb{R}^n\) with the subspace \(\varphi_i(U_i \cap V_j)\), it is open in the subspace topology on \(\varphi_i(U_i \cap V_j)\) (which, since \(\varphi_i(U_i \cap V_j)\) itself is an open set, is equivalent to saying that it is an open set in \(\mathbb{R}^n\) contained in \(\varphi_i(U_i \cap V_j)\)). Then, since the transition map \(\varphi_i \circ \psi_j^{-1}\) is smooth, it is also continuous, and so \((\varphi_i \circ \psi_j^{-1})^{-1}(\varphi_i(U \cap U_i \cap V_j)) = \psi_j(U \cap U_i \cap V_j)\) is open in the subspace topology on \(\psi(U_i \cap V_j)\), which, since \(\psi(U_i \cap V_j)\) is an open set in \(\mathbb{R}^n\), means that \(\psi_j(U \cap U_i \cap V_j)\) is open in \(\mathbb{R}^n\). Next, observe that

\begin{align}\psi_j(U \cap V_j) &= \psi_j((U \cap M) \cap V_j) \\&= \psi_j\left(U \cap \left(\bigcup_i U_i\right) \cap V_j \right) \\&= \psi_j\left(\bigcup_i(U \cap U_i \cap V_j)\right) \\&= \bigcup_i\psi_j(U \cap U_i \cap V_j).\end{align}

Thus, \(\psi_j(U \cap V_j)\) is the union of open sets in \(\mathbb{R}^n\), and hence is open in \(\mathbb{R}^n\). Thus, \(U\) is open in the topology induced by \(\mathcal{A}_2\). The same argument can be applied to show that any set open in the topology induced by \(\mathcal{A}_2\) is likewise open in the topology induced by \(\mathcal{A}_1\). Thus, the two topologies are equal.

This means that the topology induced by an atlas is well-defined, since the same topology is induced by every compatible atlas. Thus we may refer to "the" topology induced by a smooth structure.

Alternative Definition

Another definition of a smooth manifold is a topological space which is locally homeomorphic to \(\mathbb{R}^n\) which is covered by charts whose maps are homeomorphisms onto open subsets of \(\mathbb{R}^n\). This definition is equivalent.

First, note that the given topology and the induced topology will be the same topology. Suppose that \(U\) is open in the given topology. Then, for any coordinate chart \((U_i, \varphi_i)\), since \(U_i\) is open in the given topology, so is \(U \cap U_i\). Then, since \(\varphi_i\) is a homeomorphism, its inverse \(\varphi_i^{-1}\) is continuous, so \((\varphi_i^{-1})^{-1}(U \cap U_i) = \varphi_i(U \cap U_i)\) is open in \(\mathbb{R}^n\). Thus, \(U\) is open in the induced topology. Conversely, if \(U\) is open in the induced topology, then \(\varphi_i(U \cap U_i)\) is open for every chart \((U_i,\varphi_i)\). Since \(\varphi_i\) is a homeomorphism, \(\varphi_i^{-1}(\varphi_i(U \cap U_i)) = U \cap U_i\) is open in the given topology. Then, since

\begin{align}U &= U \cap M \\&= U \cap \bigcup_i U_i \\&= \bigcup_i (U \cap U_i),\end{align}

\(U\) is the union of open sets in the given topology and hence open in the given topology.

Thus, the given topology is the same as the induced topology.

Next, we want to demonstrate that the definitions are equivalent. We only need to show that the chart maps are homeomorphisms in the original definition. Since each chart map is bijective, we further only need to show that each chart map and each chart map inverse are continuous. Suppose that \(V \subset \varphi_i(U_i)\) is open in the subspace topology on \(\varphi_i(U_i)\). Since \(\varphi_i(U_i)\) is itself open in \(\mathbb{R}^n\), this means that \(V\) is open in \(\mathbb{R}^n\). Then, \(\varphi_i^{-1}(V) \subseteq U_i\). We want to show that \(\varphi_i^{-1}(V)\) is open in the induced topology on \(M\), which means that \(\varphi_j(\varphi_i^{-1}(V) \cap U_j)\) is open in \(\mathbb{R}^n\) for all charts \((U_j, \varphi_j)\). Note that, since \(\varphi_i^{-1}(V) \subseteq U_i\), it follows that \(\varphi_i^{-1}(V) = \varphi_i^{-1}(V) \cap U_i\), and so \(\varphi_i^{-1}(V) \cap U_j = \varphi_i^{-1}(V) \cap U_i \cap U_j\). Then, observe that

\begin{align}\varphi_j(\varphi_i^{-1}(V) \cap U_j) &= \varphi_j(\varphi_i^{-1}(V) \cap U_j \cap U_i) \\&= \varphi_j(\varphi_i^{-1}(V) \cap \varphi_i^{-1}(\varphi_i(U_j \cap U_i))) \\&= \varphi_j \circ \varphi_i^{-1}(V \cap \varphi_i(U_j \cap U_i)).\end{align}

The set \(\varphi_i(U_j \cap U_i)\) is open in \(\mathbb{R}^n\) by the definition of an atlas, and hence so is the intersection \(V \cap \varphi_i(U_j \cap U_i)\). The transition map \(\varphi_j \circ \varphi_i^{-1}\) is continuous, and the inverse transition map \(\varphi_i \circ \varphi_j^{-1} = (\varphi_j \circ \varphi_i^{-1})^{-1}\) is continuous also. Since \(\varphi_j \circ \varphi_i^{-1}(V \cap \varphi_i(U_j \cap U_i))\) is the inverse image of the continuous map \((\varphi_j \circ \varphi_i^{-1})^{-1}\), it is open in \(\mathbb{R}^n\). Thus, \(\varphi_j(\varphi_i^{-1}(V) \cap U_j)\) is open in \(\mathbb{R}^n\), and \(V\) is open in \(M\). Thus, \(\varphi_i\) is continuous.

Next, we want to show that \(\varphi_i^{-1}\) is continuous for each chart \((U_i,\varphi_i)\). Suppose that \(U \subseteq U_i\) is open in the subspace topology on \(U_i\). Since \(U_i\) is itself open in \(M\), this implies that \(U\) is open in \(M\) also. We want to show that \((\varphi_i^{-1})^{-1}(U) = \varphi_i(U)\) is open in the subspace topology on \(\varphi_i(U_i)\), and since \(\varphi_i(U_i)\) is itself open in \(\mathbb{R}^n\), this means that we want to show that \(\varphi_i(U)\) is open in \(\mathbb{R}^n\). Since \(U\) is open in \(M\), \(\varphi_i(U \cap U_i)\) is open in \(\mathbb{R}^n\), and, since \(U \subseteq U_i\), \(\varphi_i(U) = \varphi_i(U \cap U_i)\), and hence \(\varphi_i(U)\) is open in \(\mathbb{R}^n\). Thus, \(\varphi_i^{-1}\) is continuous.

The definition we have given is preferable in many circumstances, since it does not require one to stipulate a topology; rather, only the charts need to be specified (which is necessary in either definition anyway), and the topology is induced.

Two additional properties are usually assumed of smooth manifolds:

• the topology is (Hausdorff) separable: for every \(p,q \in M\), there exist disjoint open sets \(U,V \subseteq M\) such that \(p \in U\), \(q \in V\). This separability axiom ensures the uniqueness of limits of sequences;
• the topology is second countable (that is, there exists a countable basis for the topology)

Neither of these properties is guaranteed to be satisfied within the induced topology on a given smooth manifold. Thus, the definition of smooth manifold is often amended to include these two properties as axioms, that is, the class of manifolds considered is restricted to this class.

Smooth Maps

Next, we consider how a homomorphism (that is, a "structure-preserving" map) between smooth manifolds is defined. Consider Figure 14.

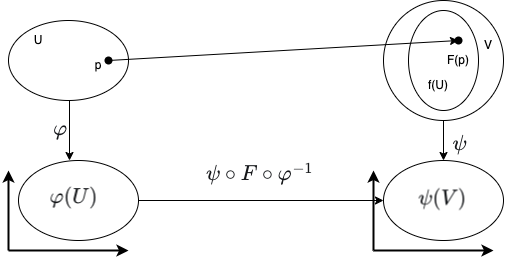
A map \(F : M \rightarrow N\) between smooth manifolds \(M\) and \(N\) is a smooth map if, for every point \(p \in M\), there exists a chart \((U,\varphi)\) on \(M\) such that \(p \in U\) and there exists a chart\((V,\psi)\) on \(N\) such that \(F(U) \subseteq V\) and \(\psi \circ F \circ \varphi^{-1}\) is a smooth function.

The map \(\widehat{F} = \psi \circ F \circ \varphi^{-1}\) is called the coordinate representation of the map \(F\) with respect to the charts \((U,\varphi)\) and \((V,\psi)\).

Thus, a map between smooth manifolds is a smooth map if its coordinate representation with respect to some pair of charts is smooth.

Chart Maps are Smooth

An immediate consequence of this definition is that every chart map is smooth. Consider a chart \((U,\varphi)\) on a smooth manifold \(M\). The set \(U\) itself may be considered as a smooth manifold with the single chart \((U,\varphi)\). Likewise, the image \(\varphi(U)\) may be considered as a smooth manifold with a single chart \((\varphi(U),\mathrm{Id}_{\varphi(U)})\). Then, for each point \(p \in U\), \(\varphi(U) \subseteq \varphi(U)\), of course, and \(\mathrm{Id}_{\varphi(U)} \circ \varphi \circ \varphi^{-1} = \mathrm{Id}_{\varphi(U)}\) is smooth.

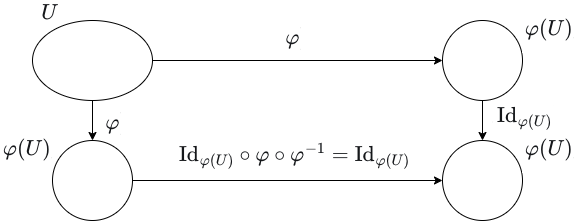
Smooth Maps are Continuous

Every smooth map \(F : M \rightarrow N\) is also continuous. Since \(F\) is smooth, for each point \(p \in M\), there exists a chart \((U,\varphi)\) on \(M\) and a chart \((V,\psi)\) on \(N\) such that \(F(U) \subseteq V\) and \(\psi \circ F \circ \varphi^{-1} : \varphi(U) \rightarrow \psi(V)\) is smooth (and hence, in particular, continuous). Since each chart map is continuous, the composite \(F\rvert_U : U \rightarrow V\) is continuous, where

\[F\rvert_U = \psi^{-1} \circ \psi \circ F \circ \varphi^{-1} \circ \varphi.\]

Since \(F\) is continuous in an open neighborhood of each point, it is continuous on all of \(M\).

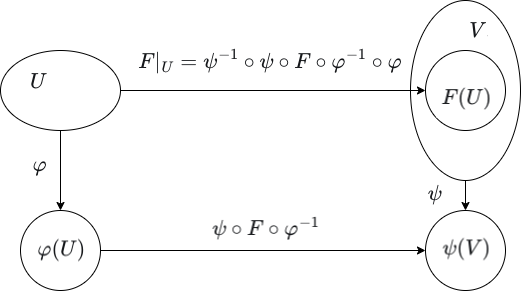
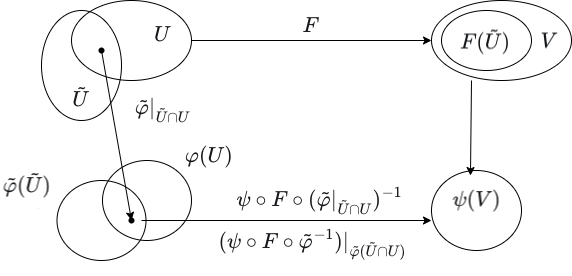
Smoothness is a Local Property

Smoothness is a local property, meaning that \(F : M \rightarrow N\) is a smooth map if and only if \(F\rvert_U : U \rightarrow N\) is a smooth map for all open sets \(U \subseteq M\). For the "if" portion, simply set \(U = M\) and thus \(F\rvert_M = F\) is smooth. For the "only if" portion, suppose \(F\) is smooth and let \(U\) be any open set in \(M\). Then, since \(F\) is smooth, there exists a chart \((\tilde{U},\tilde{\varphi})\) on \(M\) and a chart \((V,\psi)\) on \(N\) such that \(F(\tilde{U}) \subseteq V\) and \(\psi \circ F \circ \tilde{\varphi}^{-1} : \tilde{\varphi}(\tilde{U}) \rightarrow \psi(V)\) is smooth. By definition, \((\tilde{U} \cap U, \tilde{\varphi}\rvert_{\tilde{U} \cap U})\) is a chart on \(U\). Then, since

\[\psi \circ F \circ (\tilde{\varphi}\rvert_{\tilde{U} \cap U})^{-1} = (\psi \circ F \circ \tilde{\varphi}^{-1})\rvert_{\tilde{\varphi}(\tilde{U} \cap U)},\]

and the latter is smooth (since smoothness on \(\mathbb{R}^n\) is a local property and hence the restriction of a smooth function to an open subset is smooth), it follows that \(\psi \circ F \circ (\tilde{\varphi}\rvert_{\tilde{U} \cap U})^{-1}\) is smooth.

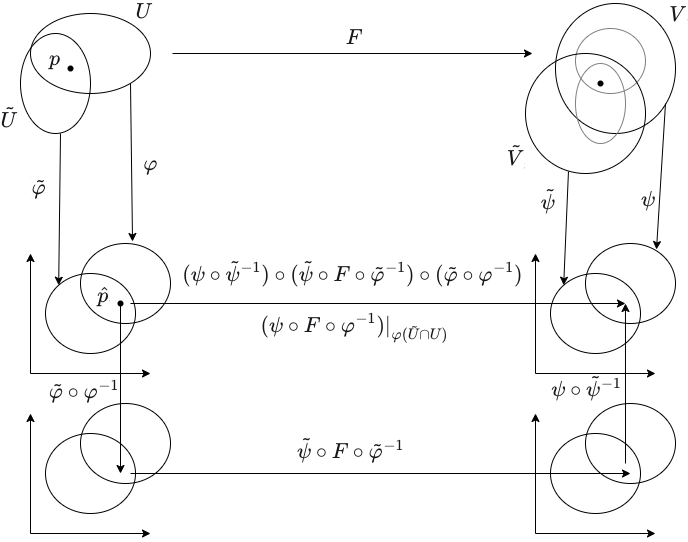
All Coordinate Representations are Smooth

Although the definition of a smooth map only requires the existence of a particular pair of charts such that the coordinate representation with respect to this pair is smooth, the coordinate representation of a smooth map with respect to any pair of charts is also smooth. Let \((U,\varphi)\) and \((V,\psi)\) be any charts for manifolds \(M\) and \(N\), respectively, and let \(F: M \rightarrow N\) be a smooth map. Let \(\hat{p}\) be any point in \(\varphi(U)\). Since \(\varphi\) is bijective, there exists a point \(p \in U\) such that \(\varphi(p) = \hat{p}\). Since \(F\) is smooth, there exists a chart \((\tilde{U},\tilde{\varphi})\) on \(M\) and a chart \((\tilde{V},\tilde{\psi})\) on \(N\) such that \(p \in \tilde{U}\) (and hence \(\hat{p} \in \varphi(\tilde{U})\)), \(F(\tilde{U}) \subseteq \tilde{V}\), and \(\tilde{\psi} \circ F \circ \tilde{\varphi}^{-1}\) is smooth. The transition maps \(\tilde{\varphi} \circ \varphi^{-1}\) and \(\psi \circ \tilde{\psi}^{-1}\) are smooth, and thus so is the composite

\[(\psi \circ \tilde{\psi}^{-1}) \circ (\tilde{\psi} \circ F \circ \tilde{\varphi}^{-1}) \circ (\tilde{\varphi} \circ \varphi^{-1}) = (\psi \circ F \circ \varphi^{-1})\rvert_{\varphi(\tilde{U} \cap U)}.\]

Thus, since, for every point \(\hat{p} \in \varphi(U)\), there exists an open neighborhood of \(\hat{p}\) such that the restriction of the corresponding coordinate representation to this open set is smooth, it follows that the coordinate representation is smooth.

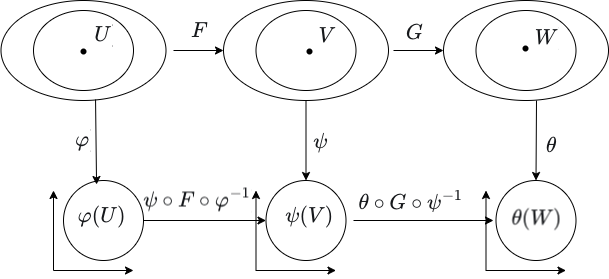
Compositions of Smooth Maps are Smooth

We can now demonstrate that the composition of smooth maps is smooth (this means that smooth manifolds and smooth maps comprise a category). Let \(F : M \rightarrow N\) and \(G : N \rightarrow P\) be smooth maps and let \(p \in M\). Since \(G\) is smooth, there exists a chart \((V,\psi)\) on \(N\) and a chart \((W,\theta)\) on \(P\) such that \(F(p) \in V\) and \(G(F(V)) \subseteq W\) and \(\theta \circ G \circ \psi^{-1} : \psi(V) \rightarrow \theta(W)\) is smooth. Since \(F\) is continuous, \(F^{-1}(V)\) is an open neighborhood of \(p\). Since \(F^{-1}(V)\) is open, its intersection with any chart is thus open and the restriction of the respective chart map to this intersection is a chart map. Thus, there exists a chart \((U, \varphi)\) for \(M\) such that \(p \in U \subseteq F^{-1}(V)\). Thus, the coordinate representation \(\psi \circ F \circ \varphi^{-1} : \varphi(U) \rightarrow \psi(V)\) is a smooth map. Then, \(G(F(U)) \subseteq G(V) \subseteq W\) and the map

\[(\theta \circ G \circ \psi^{-1}) \circ (\psi \circ F \circ \varphi^{-1}) : \varphi(U) \rightarrow \psi(W)\]

is smooth because it is the composition of smooth maps on Euclidean spaces.

Diffeomorphisms

A bijection \(F : M \rightarrow N\) such that both \(F\) and \(F^{-1}\) are smooth is called a diffeomorphism and \(M\) and \(N\) are said to be diffeomorphic. Two smooth manifolds are "the same" if they are diffeomorphic.

Every chart map is a diffeomorphism. Let \((U,\varphi)\) be a chart on a manifold \(M\), and consider \(U\) as a manifold with the sole chart \((U,\varphi)\). The chart map \(\varphi : U \rightarrow \varphi(U)\) is smooth and bijective. Let \(\hat{p}\) be any point in \(\varphi(U)\). Since \(\varphi\) is bijective, there exists a point \(p \in U\) such that \(\varphi(p) = \hat{p}\). Consider the chart \((\varphi(U),\mathrm{Id}_{\varphi(U)})\) for \(\varphi(U)\). Then \(\varphi^{-1}(\varphi(U)) = U\) and \(\varphi \circ \varphi^{-1} \circ (\mathrm{Id}_{\varphi(U)})^{-1} = \mathrm{Id}_{\varphi(U)}\) which is smooth. Thus, since \(\hat{p}\) was arbitrary, \(\varphi^{-1}\) is smooth.