Solid Angle

This post is a detailed explanation of the concept of solid angle.

Planar Angle

Before discussing solid angle, it is instructive to review the concept of planar angle first.

A planar angle is a geometric figure consisting of a point, called a vertex, and two line segments which share the vertex as a common endpoint, as in Figure 1.

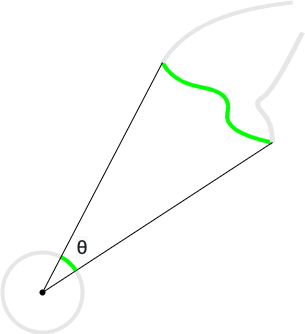
The angle subtended by a segment of a curve is the angle formed between a given vertex and two line segments extending from the vertex to two given points on the curve, as in Figure 1. If the vertex represents the center of a circle, then an arc (segment of the circle) subtends the angle, as is also depicted in Figure 1. As Figure 1 also indicates, such a curve may be a segment of a larger curve. Often, the curve segment is intended to represent the segment that is "visible" from the "vantage point" of the vertex, which is depicted in Figure 1. We may think of this as the measure of the projection of the curve onto an arc of a circle (the measure of the "shadow" cast upon the arc by the curve). Thus, we need to know how to compute this projection for an arbitrary curve.

Various measures can be defined to express the magnitude of an angle. For instance, the unit of radians expresses the ratio of arc length to the radius of a particular circle. One radian is the measure of the angle subtended by an arc on a particular circle whose length is equal to the radius of the same circle. Thus, on the unit circle, the angular measurement in radians expresses the length of the arc that subtends the angle.

Thus, in units of radians, the angular measure of the projection (i.e. arc) of a curve onto a circle of a given radius is equivalent to the angular measure of the projection of the curve onto the unit circle.

For our purposes, we will consider planar angles as a geometric figure consisting of a pair of vectors in \(\mathbb{R}^2\). The dot product (inner product) permits us to measure angle. The dot product \(a \cdot b\) satisfies the relation

\[a \cdot b = \lVert a \rVert \lVert b \rVert \cos \theta\]

where \(\theta\) is the angle formed by \(a\) and \(b\). Therefore, if both \(a\) and \(b\) are unit vectors (\(\lVert a \rVert = \lVert b \rVert = 1\)), then \(a \cdot b = \cos \theta\).

We can compute the orthogonal projection of a vector onto another: we can use the inner product, as in Figure 2.

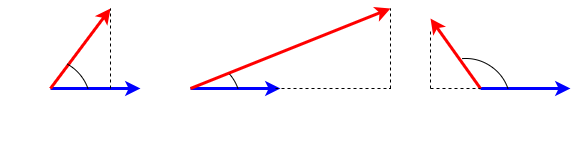
Therefore, if \(u\) is a unit vector (\(\lVert u \rVert = 1\)), then \(a \cdot u = \lVert a \rVert \cos \theta\), which computes the magnitude of the orthogonal projection. The projection itself is \((a \cdot u)u\).

We can use vectors to approximate a curve and to approximate an arc and thus compute the projection. We can select an appropriate unit tangent vector as a linear approximation for the arc and and appropriate tangent vector as a linear approximation for the curve, as in Figure 3.

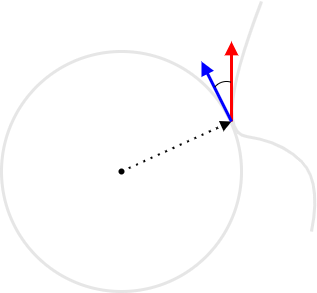
We can then compute the orthogonal projection of the curve's tangent vector onto the arc's unit tangent vector. We can define a vector field \(F : C \subseteq \mathbb{R}^2 \rightarrow \mathbb{R}^2\) such that \(F(p) = T(p)/(\lVert T(p) \rVert R)\), where \(T(p)\) represents a vector tangent to the circle with center \(o\) and radius \(R = \lVert p - o \rVert\) at the point \(p \in C\) and \(C\) is the curve (since angular measurement in radians is the ratio of arc length to radius, we must divide by \(R\)).

Note that the result depends on the orientation of the curve and circle (which way the vectors point in Figure 3). If the circle is oriented counterclockwise, then the vector \(T(x,y) = (-y, x)\) is tangent to the point \((x, y)\), but if the circle is oriented clockwise, then the vector \(T(x,y) = (x,-y)\) is tangent to the point \(x, y\).

For our present purposes, the orientation is irrelevant, and, in the end, we will derive an expression that uses the absolute value of the magnitude of the projection. Meanwhile, assume that a consistent orientation is chosen.

Thus, we can specify the following vector field:

\[F(p) = \frac{1}{\lVert p - o \rVert}\frac{1}{\lVert T(p) \rVert}T(p).\]

We can parameterize the curve as a smooth map \(r : [a, b] \rightarrow C\). Note that the derivative \(r'(t)\) can serve as the definition of the vector tangent to the point \(r(t)\) on the curve. The orientation of the parameterization (whether the interval \([a, b]\) or \([b,a]\) is used) matters, but, for our purposes, in the end, we will use absolute values, so, for now, simply assume that the orientations of circle and curve are consistent.

In parametric form, the vector field is

\[F(r(t)) = \frac{1}{R_t}\frac{T(r(t))}{\lVert T(r(t)) \rVert}\]

where \(T(r(t))\) is the specified tangent vector for the circle of radius \(R_t\) and

\[R_t = \lVert r(t) - o\rVert.\]

We can now define the projection (scaled by the inverse of \(R_t\)) to be

\[F(r(t)) \cdot r'(t).\]

Note that

\begin{align}F(r(t)) \cdot r'(t) &= \frac{1}{R_t}\frac{T(r(t))}{\lVert T(r(t)) \rVert} \cdot r'(t) \\&= \frac{1}{R_t}\frac{T(r(t))}{\lVert T(r(t)) \rVert} \cdot \frac{r'(t)}{\lVert r'(t) \rVert}\lVert r'(t) \rVert \\&= \frac{1}{R_t}\cos \theta_t \lVert r'(t) \rVert,\end{align}

where the final equality follows from the fact that the dot product of a unit vector \(u\) and a vector \(a\) is equal to \(\lVert a \rVert \cos \theta\), and the specific angle \(\theta_t\) is thus defined as

\[\cos \theta_t = \frac{T(r(t))}{\lVert T(r(t)) \rVert} \cdot \frac{r'(t)}{\lVert r'(t) \rVert}.\]

We can then compute the line integral of the vector field \(F\) as follows:

\[\int_C F(r) \cdot d\mathbf{s} = \int_a^b F(r(t)) \cdot r'(t) dt.\]

Note that this line integral, by construction, integrates precisely the integrand of interest, namely the scaled projection. Also note that

\begin{align}\int_a^b F(r(t)) \cdot r'(t) dt &= \int_a^b F(r(t)) \cdot \frac{r'(t)}{\lVert r'(t)\rVert} \lVert r'(t) \rVert dt \\&= \int_a^b \frac{1}{R_t} \cos \theta_t \lVert r'(t) \rVert dt \\&= \int_C \frac{1}{R} \cos \theta ds.\end{align}

Thus, this expression computes a line integral of a scalar field:

\[\int_C \frac{1}{R} \cos \theta ds = \int_a^b \frac{1}{R_t} \cos \theta_t \lVert r'(t) \rVert dt\].

This line integral computes the area of the projection of the curve onto the unit circle, namely, the planar angular measurement of the curve.

Next, we want to define what it means to integrate with respect to planar angle. Such an integral is an integral over the portion of the unit circle that represents the projection of the curve.

We define the vector \(\omega_t\) as follows:

\[\omega_t = \frac{r(t) - o}{\rVert r(t) - o\lVert}\]

Given a scalar field \(f : S^1 \rightarrow \mathbb{R}\), we define the integral of this scalar field with respect to planar angle as follows:

\[\int_{S^1} f(\omega) d\omega = \int_C \frac{f(\omega) \cos \theta}{R} ds = \int_a^b \frac{f(\omega_t) \cos \theta_t}{R_t}\lVert r'(t) \rVert~ dt\].

Next, we will consider what the Monte Carlo estimator for a line integral looks like. Given a set of samples \(X\) drawn from the domain of a function \(f : \mathbb{R} \rightarrow \mathbb{R}\) and a probability density function \(p\), the Monte Carlo estimator is

\[E_p[f] = \frac{1}{\lvert X \rvert}\sum_{x \in X}\frac{f(x)}{p(x)}.\]

The expected value of the estimator is exactly equal to the integral:

\begin{align}E\left[E_p[f]\right] &= E\left[ \frac{1}{\lvert X \rvert}\sum_{x \in X}\frac{f(x)}{p(x)}\right] \\&= \int_a^b \frac{1}{\lvert X \rvert}\sum_{x \in X}\frac{f(x)}{p(x)} p(x) ~dx\\&= \frac{1}{\lvert X \rvert} \lvert X \rvert \int_a^b f(x) ~dx \\&= \int_a^b f(x) ~dx.\end{align}

If we estimate the line integral

\[\int_a^b f(r(t)) \lVert r'(t) \rVert~dt\]

with respect to the probability density \(r^*p\), i.e. the pullback of \(p\) along the parameterization \(r\) which satisfies \((r^*p)(t) = p(r(t))\lVert r'(t) \rVert\), then

\begin{align}E\left[ E_{r^*p}[f \circ r]\right] &= E\left[\frac{1}{\lvert X \rvert}\sum_{t \in X}\frac{f(r(t))}{p(r(t)) \lVert r'(t) \rVert} \lVert r'(t) \rVert\right] \\&= E\left[\frac{1}{\lvert X \rvert}\sum_{t \in X}\frac{f(r(t))}{p(r(t))}\right] \\&= \int_a^b \frac{1}{\lvert X \rvert}\sum_{t \in X}\frac{f(r(t))}{p(r(t))} p(r(t)) \lVert r'(t) \rVert~dt \\&= \int_a^b \frac{1}{\lvert X \rvert}\sum_{t \in X} f(r(t)) \lVert r'(t) \rVert~dt \\&= \int_a^b f(r(t)) \lVert r'(t) \rVert~dt.\end{align}

We can also define probability densities with respect to planar angle; such a density is any function \(p\) such that

\[\int_a^b \frac{p_{\omega}(\omega_t) \cos \theta_t}{R_t}\lVert r'(t) \rVert~ dt = 1.\]

We can then define a probability density \(p_L\) as follows:

\[p_L(r(t)) = \frac{p_{\omega}(\omega_t) \cos \theta_t}{R_t}\]

This means that

\[\int_a^b p_L(r(t))\lVert r'(t) \rVert~ dt = 1\]

and thus \(p_L\) is a probability density with respect to curve length. Thus, given a density for planar angle, we can derive a density for curve length.

The Monte Carlo estimator yields

\begin{align}E_{r^*p}[f] &= \frac{1}{\lvert X \rvert}\sum_{t \in X} \frac{f(\omega_t) \frac{1}{R_t}\cos \theta_t }{(r^*p)(t)}\lVert r'(t) \rVert \\&= \frac{1}{\lvert X \rvert}\sum_{t \in X} \frac{f(\omega_t) \frac{1}{R_t}\cos \theta_t }{\lVert r'(t) \rVert p_L (r(t))}\lVert r'(t) \rVert \\&= \frac{1}{\lvert X \rvert}\sum_{t \in X} \frac{f(\omega_t) \frac{1}{R_t}\cos \theta_t }{ p_L (r(t))} \\&= \frac{1}{\lvert X \rvert}\sum_{t \in X} \frac{f(\omega_t) \frac{1}{R_t}\cos \theta_t }{ p_{\omega} (\omega_t) \frac{1}{R_t}\cos \theta_t} \\&= \frac{1}{\lvert X \rvert}\sum_{t \in X} \frac{f(\omega_t)}{p_{\omega}(\omega_t)}.\end{align}

Solid Angle

Solid angle is the generalization of planar angle to three dimensions. When restricted to spheres, solid angle can be conceived as a geometric figure which resembles a cone terminating in a spherical cap, as in Figure 11.

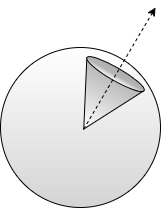
However, due to the difficulty of defining such a figure precisely for more general surfaces, we only define the measure of solid angle (and often simply refer to this measure as "solid angle"). Just as the measure of the planar angle subtended by a curve is the measure of the arc length of the projection of a curve onto the unit circle, the measure of solid angle is analogously the measure of the area of the projection of an arbitrary surface onto the unit sphere, as in Figure 12. The surface is said to subtend the solid angle at the given apex (center of the unit sphere). Unlike planar angle, where the projection of a curve onto the unit circle is always in the shape of an arc, the projection of a surface onto the unit sphere can assume an arbitrary shape. This is analogous to the "shadow" of the shape.

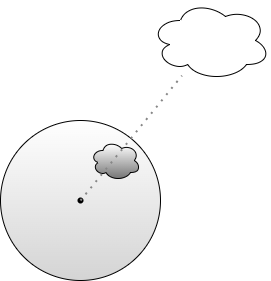
The measure of solid angle is expressed in units of steradians. One steradian is defined as the ratio of the area of the solid angle subtended by a given surface at the center of a given sphere to the square of the radius of the sphere (since the surface area of a sphere is proportional to the square of its radius). Thus, on a unit sphere (i.e. the sphere with radius \(1\)), the unit of steradians measures the area of the solid angle subtended by a surface. In other words, on the unit sphere, the unit of steradians measures the area of the projection of the surface onto the unit sphere.

Throughout our discussion, we will make several simplifying assumptions so that these details will not serve as a distraction:

1. We are only considering a single surface.
2. The entirety of the surface is "visible" from the given apex (i.e. there are no "folds" of the surface which are occluded by another portion of the surface).
3. No other intermediate object occludes the surface (there is no object between the apex and each point on the surface under consideration).
4. We will neglect the fact that the scene might be open (i.e. the surface of the unit sphere might not be completely covered by projections from other surfaces).

We will relax these assumptions after we introduce numerical integration.

Thus, we need to be able to calculate this projection for arbitrary surfaces. Figure 13 depicts the approximation to the projection at a point.

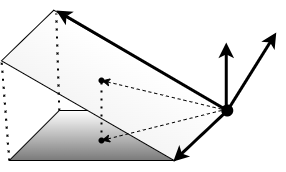
Each surface \(S\) has a parameterization \(r(s,t) : T \rightarrow S\), where \(T\) is a Euclidean (flat, rectangular) domain (rectangular subset of \(\mathbb{R}^2\)). At each point \(p\) on the surface, we define a facet which approximates the area of the surface near the point. This facet is a parallelogram spanned by the tangent vectors \(\partial/\partial s\rvert_p\) and \(\partial/\partial t\rvert_p\) emanating from the point \(p\). We can also define the normal vector at the point as \(\mathbf{n}_p = \partial/\partial s\rvert_p \times \partial/\partial t\rvert_p\). Every point on the facet is orthogonal to \(\mathbf{n}_p\) and \(\mathbf{n}_p\) is orthogonal to both \(\partial/\partial s\rvert_p\) and \(\partial/\partial t\rvert_p\). We fix a given apex \(o\) and consider the sphere with center \(o\) and radius \(\lVert p - o \rVert\) so that the point \(p\) also lies on the surface of this sphere. We want to define the area of the projection of this facet onto a plane that is tangent at this point to this sphere. We can also define a unit vector \(N(p)\) normal to the sphere at this point (and hence normal to the tangent plane at this point also). The angle between \(N(p)\) and \(\mathbf{n}_p\) is the same as the angle between each point on the facet and its projection onto the tangent plane. Since the magnitude of the cross product of any two vectors is equal to the area of the parallelogram spanned by the vectors, the cross product \(\mathbf{n}_p = \partial/\partial s\rvert_p \times \partial/\partial t\rvert_p\) of the facet's spanning vectors has a magnitude which is equal to the area of the facet. Thus, in a sense, \(\mathbf{n}_p\) represents the facet and \(N(p)\) represents the tangent plane. Thus, the magnitude of the projection of \(\mathbf{n}_p\) onto \(N(p)\) is equal to the area of the projection of the facet onto a plane tangent to the sphere. This projection can be computed via the dot product as

\[\left(\frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p\right) \cdot N(p) = \left\lVert \frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p\right\rVert \lVert N(p) \rVert \cos \theta_p = \left\lVert \frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p \right\rVert \cos \theta_p,\]

where \(\theta_p\) is the measure of the angle between the normal vectors, and is thus defined such that

\[\cos \theta_p = N(p) \cdot \frac{\frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p}{\bigg\lVert\frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p\bigg\rVert}.\]

The unit vector normal to a sphere with center \(o\) at point \(p\) is defined as

\[N(p) = \frac{p - o}{\lVert p - o \rVert}.\]

The radius of the sphere at point \(p\) is thus defined as

\[R_p = \lVert p - o \rVert.\]

Since the measure of solid angle on the sphere is the ratio of this projection to the square of the radius of the sphere, the measure of the solid angle is thus

\[\frac{1}{R_p^2}\left(\frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p\right) \cdot N(p) = \frac{1}{R_p^2}\left\lVert \frac{\partial}{\partial s}\bigg\rvert_p \times \frac{\partial}{\partial t}\bigg\rvert_p \right\rVert\cos \theta_p.\]

Thus, if we define a vector field \(F : S \rightarrow \mathbb{R}^2\) as

\[F(p) = \frac{1}{R_p^2}N(p),\]

then the surface integral of this vector field computes the solid angle as

\begin{align}\iint_S F \cdot ~d\mathbf{s} &= \iint_S F \cdot \mathbf{n} ~ds \\&= \iint_T F(r(s,t)) \cdot \left(\frac{\partial}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial}{\partial t}\bigg\rvert_{r(s,t)}\right) ~ds~dt.\end{align}

We can also write this integral as

\begin{align}\iint_T F(r(s,t)) \cdot \left(\frac{\partial r}{\partial s} \times \frac{\partial r}{\partial t} \right) ~ds~dt &= \iint_T \frac{1}{R_{(s,t)}^2}N(r(s,t))\cdot \left(\frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \right) ~ds~dt \\&= \iint_T \frac{1}{R_{r(s,t)}^2}N(r(s,t))\cdot \frac{\left(\frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \right)}{\bigg\lVert \frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \bigg\rVert } \bigg\lVert \frac{\partial r}{\partial s} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)}\bigg\rVert ~ds~dt \\&= \iint_T \frac{1}{R_{r(s,t)}^2}\cos \theta_{r(s,t)} \left\lVert \frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \right\rVert ~ds~dt. \end{align}

Thus, if we define a scalar field \(F : T \rightarrow \mathbb{R}\) as

\[F(p) = \frac{1}{R_p^2} \cos \theta_p\],

then this integral also computes the integral of this scalar field:

\begin{align}\iint_S F dS &= \iint_T F(r(s,t)) \bigg\rVert \frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \bigg\lVert~ds~dt \\&= \iint_T \frac{1}{R_{r(s,t)}^2}\cos \theta_{r(s,t)} \left\lVert \frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \right\rVert ~ds~dt .\end{align}

The integral over this scalar field is often abbreviated as

\[\int_A \frac{1}{R^2}\cos \theta ~dA.\]

In this abbreviation, the \(A\) represents "area", and the parameters are suppressed, i.e. \(\theta\), \(R\), and \(\omega\) are functions that compute values for each point on the surface. This notation is employed since it is economical.

This defines a particular volume measure which can be used for integrating functions.

Thus, given any function \(f : S \rightarrow \mathbb{R}\), we define the integral with respect to surface area as

\begin{align}\iint_S f~dS &= \iint_S f (\frac{1}{R^2} \cos \theta) dS \\&= \iint_T f(r(s,t)) \frac{1}{R_{r(s,t)}^2} \cos \theta_{r(s,t)} \left\lVert \frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \right\rVert ~ds ~dt.\end{align}

The integral with respect to solid angle is simply the integral of a function whose support is precisely the solid angle of some surface (i.e. the projection of the surface onto the unit sphere) over the unit sphere (see this post for a derivation):

\begin{align}\iint_\Omega f ~d\omega = \int_0^{2\pi}\int_0^{\pi} f(r(\varphi,\theta)) \sin \varphi ~d\varphi~d\theta.\end{align}

In other words, \(f(p) = 0\) for any point \(p\) outside the projection of the surface onto the unit sphere, and \(f(p)\) is only non-zero within the projection.

We can compute the point \(\omega(p)\) on the unit sphere with center \(o\) corresponding to a point \(p\) on a surface \(S\) as

\[\omega(p) = \frac{p - o}{\lVert p - o \rVert}.\]

Given a function \(f\) defined on the unit sphere, we can convert to an integral over area as follows:

\begin{align}\iint_\Omega f ~d\omega &= \iint_S f(\omega) (\frac{1}{R^2} \cos \theta) dS \\&= \iint_T f(\omega(r(s,t)) \frac{1}{R_{r(s,t)}^2} \cos \theta_{r(s,t)} \left\lVert \frac{\partial r}{\partial s}\bigg\rvert_{r(s,t)} \times \frac{\partial r}{\partial t}\bigg\rvert_{r(s,t)} \right\rVert ~ds ~dt.\end{align}

This equivalence is often abbreviated as

\[\int_{\S^2} f ~d\omega = \int_{A}f(\omega) \frac{1}{R^2}\cos \theta~dA.\]

Thus, both integrals are related to solid angle, but one performs the integration over the unit sphere as a domain, and the other performs the integration over the surface as a domain. There is a geometric conversion factor of \(\cos \theta / R^2\) which accounts for the projection; this is not a Jacobian determinant (found in change of variables formulas from calculus).

Let's consider a simple example. Let's compute the solid angle of a sphere with radius \(2\) (as projected on a unit sphere centered at the same apex). It should cover the entire unit sphere, and hence be equal to the surface area of the unit sphere, which is \(4\pi\). If we denote the unit sphere as \(S^2\) and the sphere with radius \(2\) as \(A\) and the parameterization of \(S^2\) in terms of spherical coordinates as \(r(s,t)\), then, since \(R\) is \(2\) at each point and \(\cos \theta\) is \(1\) at each point (since the respective unit normal vectors coincide and the angle between them is \(0\) radians), we compute

\begin{align}\int_{S^2} d\omega &= \int_{A} \frac{1}{R^2}\cos \theta dA \\&= \int_0^{2\pi}\int_0^{\pi} \frac{1}{R_{r(s,t)}^2} \cos \theta_{r(s,t)} R^2 \sin s ~ds ~dt \\&= \int_0^{2\pi}\int_0^{\pi} \sin s ~ds ~dt \\&= 4\pi.\end{align}

Of course, we could have computed the surface area of the sphere with radius \(2\) directly; this calculation is simply a verification that shows that we have computed the projection correctly in this instance.