Metric Tensor Fields

This post is about metric tensor fields on smooth manifolds, which permit the introduction of geometry to smooth manifolds.

This post considers both the Riemannian and semi-Riemannian cases.

Note that the summation convention is used throughout this post.

Inner Product Spaces

An important operation available on certain vector spaces is the inner product.

The Dot Product

The standard example of an inner product is the Euclidean dot product. For any vectors \(v,w \in \mathbb{R}^n\) expressed as \(v = v^ie_i\) and \(w = w^je_j\) in terms of the standard basis \((e_1,\dots,e_n)\), the dot product is defined so that

\[v \cdot w = v^iw^j \delta_{ij} = \sum_{i=1}^n v^iw^i,\]

where \(\delta_{ij}\) is the Kronecker delta defined such that

\[\delta_{ij} = \begin{cases}1 & \text{if \(i = j\),} \\ 0 & \text{otherwise},\end{cases}\]

which permits us to write expressions using the summation convention. This product can also be written in bracket notation:

\[v \cdot w = \langle v,w \rangle.\]

Note that the dot product is symmetric, i.e.

\[\langle v,w \rangle = \langle w,v \rangle\]

as a consequence of the commutativity of real multiplication.

Note also that

\begin{align}\langle av, w \rangle &= \sum_{i=1}^n (av^i)w^i \\&= a\sum_{i=1}^n v^iw^i \\&= a \langle v,w \rangle,\end{align}

and

\begin{align}\langle v + w, x \rangle &= \sum_{i=1}^n (v^i + w^i)x^i \\&= \sum_{i=1}^n (v^ix^i + w^ix^i) \\&= \left(\sum_{i=1}^n v^ix^i \right) + \left(\sum_{i=1}^n w^ix^i \right) \\&= \langle v, x \rangle + \langle w, x \rangle, \end{align}

and similar relations obtain in the second argument, which together imply that the dot product is a bilinear operation.

Finally, note that the dot product is positive definite, i.e. \(\langle v,v \rangle \gt 0\) whenever \(v \neq 0\) and \(\langle 0, 0 \rangle = 0\).

The length \(\lvert v \rvert\) of a vector \(v \in \mathbb{R}^n\) can be computed as

\[\lvert v \rvert = \langle v,v \rangle^{\frac{1}{2}} = \left((v^1)^2 + \dots + (v^n)^2\right)^{\frac{1}{2}}.\]

The dot product has a geometric interpretation. It can alternatively be defined as

\[v \cdot w = \lvert v \rvert \lvert w \rvert \cos \theta,\]

where \(\theta\) is the measure of the angle formed by \(v\) and \(w\).

This definition is bilinear, as can be established by a geometric argument (see Figure 2).

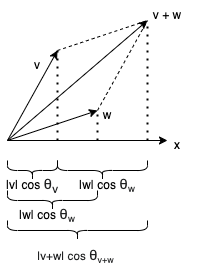
This figure indicates that

\[\lvert v \rvert \cos \theta_v + \lvert w \rvert \cos \theta_w = \lvert v + w \rvert \cos \theta_{v+w},\]

which then implies

\begin{align}(v+w) \cdot x &= \lvert v + w \rvert \lvert x \rvert \cos \theta_{v+w} \\&= (\lvert v \rvert \cos \theta_v + \lvert w \rvert \cos \theta_w) \lvert x \rvert \\&= \lvert v \rvert \lvert x \rvert \cos \theta_v + \lvert w \lvert x \rvert \rvert \cos \theta_w \\&= v \cdot x + w \cdot x.\end{align}

It also follows that

\begin{align}v \cdot e_i &= \lvert v \rvert \lvert e_i \rvert \cos \theta \\&= \lvert v \rvert \cos \theta_i \\&= v^i.\end{align}

Thus, using the properties of the geometric dot product, we can adduce that it is equivalent to the algebraic dot product:

\begin{align}v \cdot w &= v \cdot (w^ie_i) \\&= w^i (v \cdot e_i) \\&= \sum_{i=1}^n v^iw^i.\end{align}

Inner Products

Given a real vector space \(V\), an inner product on \(V\) is a map \(\langle -,-\rangle : V \times V \rightarrow \mathbb{R}\) (i.e., if \(v,w \in V\), then \(\langle v,w \rangle \in \mathbb{R}\)) that satisfies the following properties (where \(v,w,x \in V\) and \(a,b \in \mathbb{R}\)):

• Symmetry: \(\langle v,w \rangle = \langle w,v \rangle\).
• Bilinearity:
  • \(\langle av,w \rangle = a \langle v,w \rangle\) and \(\langle v, bw \rangle = b \langle v, w\rangle\).
  • \(\langle v + w, x \rangle = \langle v, x \rangle + \langle w, x \rangle\) and \(\langle v, w + x \rangle = \langle v, w \rangle + \langle v, x \rangle\).
• Positive Definiteness: \(\langle v, v \rangle \gt 0\) if \(v \neq 0\), and \(\langle 0, 0 \rangle = 0\).

The combination of a vector space with a given inner product is called an inner product space.

The inner product alone is enough to compute various important geometric quantities.

Length

The length or norm of a vector \(v \in V\) is the quantity \(\lvert v \rvert \in \mathbb{R}\) defined as follows:

\[\lvert v \rvert = \langle v,v \rangle^{\frac{1}{2}}.\]

Norms on Vector Spaces

A norm on a vector space \(V\) is a map \(\lvert - \rvert : V \rightarrow \mathbb{R}\) which satisfies the following properties for all \(v,w \in V\) and \(a \in \mathbb{R}\):

• Triangle Inequality: \(\lvert v + w \rvert \leq \lvert v \rvert + \lvert w \rvert\).
• Absolute Homogeneity: \(\lvert av \rvert = \lvert a \rvert \lvert v \rvert\) (where \(\lvert a \rvert\) is a norm on \(\mathbb{R}\), namely, the absolute value).
• Positive Definiteness: \(\lvert v \rvert \gt 0\) if \(v \neq 0\), and \(\lvert 0 \rvert = 0\).

Actually, a weaker condition can be defined for positive definiteness which is equivalent since the above condition is implied by the other conditions: if \(\lvert v \rvert = 0\), then \(v = 0\).

The Cauchy-Schwarz Inequality states that \(\langle v, w \rangle \leq \langle v,v \rangle \langle w, w \rangle\). Using this property, we can demonstrate that the norm induced by an inner product satisfies the triangle inequality, since

\begin{align}\lvert v + w \rvert &= (\lvert v + w \rvert^2)^{\frac{1}{2}} \\&= \langle v+w,v+w \rangle^{\frac{1}{2}} \\&= (\langle u,u\rangle + \langle v,w \rangle + \langle w,v \rangle + \langle w,w \rangle)^{\frac{1}{2}} \\&= (\langle u,u\rangle + 2\langle v,w \rangle + \langle w,w \rangle)^{\frac{1}{2}} \\&\leq (\langle u,u\rangle + 2\langle v,v \rangle \langle w,w \rangle + \langle w,w \rangle)^{\frac{1}{2}} & \text{(By the Cauchy-Schwarz Inequality)} \\&= (\lvert v \rvert + 2\lvert v \rvert \lvert w \rvert + \lvert w \rvert)^{\frac{1}{2}} \\&= ((\lvert v \rvert + \lvert w \rvert)^2)^{\frac{1}{2}} \\&= \lvert v \rvert + \lvert w \rvert.\end{align}

The induced norm satisfies absolute homogeneity, since

\begin{align}\lvert av \rvert &= \langle av, av \rangle^{\frac{1}{2}} \\&= (a^2\langle v,v \rangle)^{\frac{1}{2}} \\&= (a^2)^{\frac{1}{2}}(\langle v,v \rangle)^{\frac{1}{2}} \\&= \lvert a \rvert \lvert v \rvert.\end{align}

The positive definiteness of the induced norm follows immediately from the positive definiteness of the inner product.

Thus, each inner product induces a norm.

A vector space together with a norm is called a normed vector space.

Polarization Identity

The converse is also true: each norm induces an inner product. Consider the following calculation:

\begin{align}\frac{1}{4}\left[\langle v + w, v + w \rangle - \langle v -w, v - w \rangle \right] &= \frac{1}{4}\left[ \langle v +w, v + w \rangle + \langle v - w, w - v \rangle\right] \\&= \frac{1}{4} \left[ \langle v+w+(v-w), v+w+(w-v)\rangle \right] \\&= \frac{1}{4} \langle 2v, 2w \rangle \\&= \langle v, w \rangle.\end{align}

Thus, it follows that, given a norm, we can define an inner product as follows:

\[\langle v,w \rangle = \frac{1}{4}\left( \lvert v + w \rvert - \lvert v - w \rvert \right).\]

Angle

The angle between two nonzero vectors \(v,w \in V\) is defined as the unique angle \(\theta \in [0,\pi]\) satisfying the following relationship:

\[\cos \theta = \frac{\langle v,w \rangle}{\lvert v\rvert \lvert w \rvert}.\]

Two vectors are orthogonal if \(\langle v,w \rangle = 0\). This occurs precisely when either of the vectors is \(0\), or else the angle between them is \(\pi/2\).

A basis \((E_1,\dots,E_n)\) for an inner product space is called orthonormal if \(\langle E_i,E_j \rangle = \delta^i_j\), which means that each vector has length \(1\) (i.e. \(\lvert E_i \rvert = 1\)) and each of the vectors is pairwise orthogonal (when \(i \neq j\), \(\langle E_i,E_j \rangle = 0\)).

Given a vector \(v\) and a unit vector \(u\) (i.e. \(\lvert u \rvert = 1\)), the angle between them is thus

\[\cos \theta = \frac{\langle v,u \rangle}{\lvert v\rvert \lvert u \rvert} = \frac{\langle v,u \rangle}{\lvert v \rvert},\]

which implies that

\[\lvert v \rvert \cos \theta = \langle v,u \rangle.\]

Thus, the inner product \(\langle v,u \rangle\) computes the length of the adjacent leg (relative to the angle \(\theta\)) of a right triangle in which \(v\) is the hypotenuse and adjacent leg lies along the direction of \(u\). The adjacent leg can then be computed by scaling the direction \(u\) by the magnitude \(\langle v,u \rangle\), i.e. by the expression

\[\langle v,u \rangle u.\]

This is called the orthogonal projection of the vector \(v\) in the direction of \(u\).

Note that, since \(\lvert u \rvert = 1 = \langle u,u \rangle^{\frac{1}{2}}\), it follows that \(\langle u, u \rangle = 1\), and thus

\begin{align}\langle u, v - \langle v, u \rangle u \rangle &= \langle u,v \rangle - \langle \langle v,u \rangle u\rangle \\&= \langle u,v \rangle - \langle v,u \rangle \langle u, u \rangle \\&= \langle u,v \rangle - \langle v, u \rangle \\&= \langle u,v \rangle - \langle u,v \rangle \\&= 0.\end{align}

This means that the vector \(v - \langle v,u \rangle u\) is orthogonal to \(u\). The vector \(v - \langle v,u \rangle u\) can be thought of as the completion of the triangle (i.e. a vector that has the same direction and magnitude as the opposite leg of the right triangle, yet emanates from the origin, thus, when translated appropriately, it forms the opposite leg of the right triangle). See Figure 1 for an illustration.

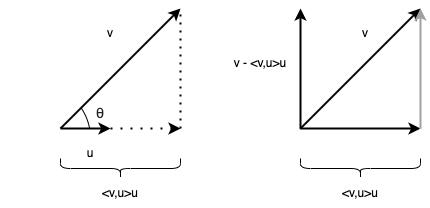
The vector \(v - \langle v,u \rangle u\) can then be normalized to yield a unit vector orthogonal to \(u\):

\[\frac{v - \langle v,u \rangle u}{\lvert v - \langle v,u \rangle u \rvert}.\]

This process guarantees that the produced vector is orthogonal to a single given vector. However, the same process can be used to devise a vector that is orthogonal to multiple vectors. Suppose that we have two unit vectors \(u_1\) and \(u_2\) each of which is orthogonal to the other. Then consider the following vector:

\[v - \langle v, u_1 \rangle u_1 - \langle v, u_2 \rangle u_2.\]

This vector is orthogonal to both \(u_1\) and \(u_2\), as can be verified by the following calculation:

\begin{align}\langle u_1, v - \langle v, u_1 \rangle u_1 - \langle v, u_2 \rangle u_2 \rangle &= \langle u_1,v \rangle + \langle u_1,-\langle v, u_1 \rangle u_1 -\langle v, u_2 \rangle u_2\rangle \\&= \langle u_1,v \rangle + \langle u_1,-\langle v, u_1 \rangle u_1 \rangle + \langle u_1, -\langle v, u_2 \rangle u_2 \rangle \\&= \langle u_1,v \rangle -\langle v, u_1 \rangle\langle u_1, u_1 \rangle -\langle v, u_2 \rangle \langle u_1, u_2 \rangle \\&= \langle u_1,v \rangle -\langle v, u_1 \rangle \\&= 0\end{align}

The penultimate step used the fact that \(\langle u_1, u_1 \rangle = 1\) and \(\langle u_1, u_2 \rangle = 0\). A similar calculation shows that this vector is orthogonal to \(u_2\) as well. This process can be repeated for any number of vectors.

This yields a recursive algorithm, called the Gram-Schmidt Algorithm, for producing an orthonormal basis \((\hat{E_1},\dots,\hat{E_n})\) from a given basis \((E_1,\dots,E_n)\) for a given vector space \(V\) with \(\mathrm{dim}(V) = n\) such that the spanning set of the two bases is the same, i.e. \(\mathrm{span}(E_1,\dots,E_n) = \mathrm{span}(\hat{E_1},\dots,\hat{E_n})\).

The first vector of the orthonormal basis is produced by normalizing the first vector of the original basis:

\[\hat{E_1} = \frac{E_1}{\lvert E_1 \rvert}.\]

For all \(j\) such that \(2 \leq j \leq \mathrm{dim}(V)\), we compute a vector orthogonal to each of the previously computed vectors and then normalize this vector:

\[\hat{E_j} = \frac{E_j - \sum_{i=1}^{j-1} \langle E_j, \hat{E_i} \rangle \hat{E_i}}{\lvert E_j - \sum_{i=1}^{j-1} \langle E_j, \hat{E_i} \rangle \hat{E_i} \rvert}.\]

Isometries

A homomorphism of inner product spaces is a linear map \(F: V \rightarrow W\) between vector spaces \(V\) and \(W\) (equipped with respective inner products \(\langle -,- \rangle_V\) and \(\langle -,- \rangle_W\)) which preserves inner products, i.e.

\[\langle F(v), F(w) \rangle_W = \langle v,w \rangle_V\]

for all \(v,w \in V\). An important case is a linear isometry, which is a homomorphism which is also an isomorphism (as a linear map of vector spaces, i.e. a vector space isomorphism).

Recall that, if a linear map \(F : V \rightarrow W\) between vector spaces of the same dimension sends basis vectors to basis vectors, then it is a linear isomorphism. Such a map determines an inverse \(F^{-1} : W \rightarrow V\) which likewise sends basis vectors to basis vectors (and linear maps are completely determined by their actions on basis vectors). Given a basis \((E^V_i)\) for \(V\) and a basis \((E^W_i)\) for \(W\), we can compute

\begin{align}F(F^{-1}(v^iE^W_i)) &= F(v^iF^{-1}(E^W_i)) \\&= F(v^iE^V_i) \\&= v^iF(E^V_i) \\&= v^iE^W_i.\end{align}

Likewise, a similar calculation shows that \(F^{-1}(F(v^iE^V_i)) = v^iE^V_i\).

A homomorphism \(F : V \rightarrow W\) of inner product spaces that maps an orthonormal basis \((\hat{E}^V_i)\) to an orthonormal basis \((\hat{E}^W_i)\) is likewise a linear isometry, which implies that all inner product spaces of the same dimension are linearly isometric to each other. This can be seen by the following calculation:

\begin{align}\langle F(v^i\hat{E}^V_i),F(w^j\hat{E}^V_j) \rangle \\&= \langle v^iF(\hat{E}^V_i),w^jF(\hat{E}^V_j) \rangle \\&= \langle v^i\hat{E}^W_i,w^j\hat{E}^W_j \rangle \\&= v^iw^j\langle \hat{E}^W_i,\hat{E}^W_j \rangle \\&= v^iw^j \delta_{ij} \\&= v^iw^j \langle \hat{E}^V_i,\hat{E}^V_j \rangle \\&= \langle v^i\hat{E}^V_i,w^j\hat{E}^V_j \rangle.\end{align}

Duality

We will sometimes write an inner product on a vector space \(V\) as a bilinear map (concrete covariant \(2\)-tensor) \(g : V \times V \rightarrow \mathbb{R}\):

\[g(v, w) = \langle v, w \rangle.\]

This induces a corresponding linear map \(\hat{g} : V \rightarrow V^*\) (the "curried" version of \(g\)):

\[\hat{g}(v)(w) = g(v, w) = \langle v,w \rangle.\]

The map \(\hat{g}\) is an isomorphism (and thus \(V \cong V^*\)) which may also be written as \(v \mapsto \langle v, - \rangle\) or \(v \mapsto g(v,-)\).

The positive definiteness of the inner product causes \(\hat{g}\) to be an isomorphism. To see this, note that the zero element of \(V^*\) is the constant map \(v \mapsto 0\). Since the inner product is positive definite, the only element mapped to the zero map is the zero element \(0 \in V\) since \(\langle 0, v \rangle = 0\) for all \(v \in V\). Thus, the kernel of \(\hat{g}\) is trivial, which implies that \(\hat{g}\) is an isomorphism.

The notation \(v^{\flat} \in V^*\) (read "v flat") is also used (and so \((-)^{\flat} = \hat{g}(-)\)):

\[v^{\flat} = \hat{g}(v) = g(v,-) = \langle v, - \rangle.\]

The notation \(\omega^{\sharp}\) (read "omega sharp") is used for the inverse map \(\hat{g}^{-1} : V^* \rightarrow V\), and so \((-)^{\sharp} = \hat{g}^{-1}(-)\). The inverse function often is not explicitly defined (indeed, there are many choices, one for each basis). However, the following relations are necessarily satisfied since the flat and sharp operations are mutual inverses:

\[(v^{\flat})^{\sharp} = v, \text{and} ~(\omega^{\sharp})^{\flat} = \omega,\]

that is,

\[\langle v, -\rangle^{\sharp} = v, \text{and} ~\langle \omega^{\sharp}, - \rangle = \omega.\]

The flat and sharp operations are often expressed in coordinates. Recall that, for any linear map \(F : V \rightarrow W \) between an \(n\)-dimensional real vector space \(V\) and an \(m\)-dimensional real vector space \(W\), given a basis \((E^V_1,\dots,E^V_n)\) for \(V\) and a basis \((E^W_1,\dots,E^W_m)\) for \(W\), the map \(F\) can be represented with respect to these bases using a matrix of coefficients as follows:

\[\begin{bmatrix}F^1(E^V_1) & \dots & F^1(E^V_n) \\ \vdots & \ddots & \vdots \\ F^m(E^V_1) & \dots & F^m(E^V_n)\end{bmatrix}.\]

This is because, for any vector \(v = v^jE^V_j \in V\),

\begin{align}F(v) &= F(v^jE^V_j) \\&= v^jF(E^V_j) \\&= v^jF^i(E^V_j)E^W_i\end{align}

since, by definition, \(F(E^V_j) = F^i(E^V_j)E^W_i\), and thus

\[\begin{bmatrix}F^1(E^V_1) & \dots & F^1(E^V_n) \\ \vdots & \ddots & \vdots \\ F^m(E^V_1) & \dots & F^m(E^V_n)\end{bmatrix} \begin{bmatrix}v^1 \\ \vdots \\ v^n\end{bmatrix} = \begin{bmatrix}v^jF^1(E^V_j) \\ \vdots \\ v^jF^m(E^V_j)\end{bmatrix}.\]

Thus, the matrix representation of \(F\) is written as

\[F_{ij} = F^i_j = F^i(E^V_j),\]

where index \(i\) represents the \(i\)-th row and index \(j\) represents the \(j\)-th column. The map \(F\) can thus be written as

\[F(v) = F^i_jv^jE^W_i.\]

We can apply this same analysis to the linear map \(\hat{g}\). Given a basis \((E_1,\dots,E_n)\) for \(V\) and the corresponding dual basis \((\varepsilon^1,\dots,\varepsilon^n)\) for \(V^*\), the map \(\hat{g}\) is represented as follows:

\[\hat{g}(v) = g_{ij}v^j\varepsilon^i,\]

where

\[g_{ij} = \hat{g}_j(E_i),\]

and, by definition,

\[\hat{g}(v) = \hat{g}_j(v)\varepsilon^j\].

Note that we have changed the position of the indices accordingly since we are dealing with dual spaces. Also note that the matrix \(g_{ij}\) is a symmetric matrix (i.e. \(g_{ij} = g_{ji}\)) since \(g\) is symmetric.

Recall that the components of any covector \(\omega \in V^*\) can be determined as

\[\omega = \omega(E_j)\varepsilon^j = \omega_j\varepsilon^j,\]

where, by definition, \(\omega_j = \omega(E_j)\).

Thus, for any vector \(v \in V\), the covector \(\hat{g}(v) \in V^*\) can be written as

\[\hat{g}(v) = \hat{g}(v)(E_j)\varepsilon^j.\]

By definition, it is also the case that

\[\hat{g}(v) = \hat{g}_j(v)\varepsilon^j,\]

and so

\[\hat{g}_j(v)\varepsilon^j = \hat{g}(v)(E_j)\varepsilon^j\],

and thus

\[\hat{g}_j(v) = \hat{g}(v)(E_j).\]

Thus

\[\hat{g}_j(v) = \hat{g}(v)(E_j) = g(v, E_j) = \langle v, E_j \rangle.\]

Thus, we have determined that

\[g_{ij} = \hat{g}_j(E_i) = g(E_i,E_j).\]

The components of the tensor \(g\) are computed as

\[g_{ij} = g(E_i,E_j).\]

Thus, the components of the tensor \(g\) and the linear map \(\hat{g}\) coincide. For this reason, the notation \(g_{ij}\) (not \(\hat{g}_{ij}\)) is used.

Now, if we write

\[v_i = g_{ij}v^j,\]

then we can also write

\[v^{\flat} = \hat{g}(v) = g_{ij}v^j\varepsilon^i = v_i\varepsilon^i.\]

Note that the index \(j\) was "lowered", i.e. was written as a subscript (\(i\)) in the latter expression but a superscript (\(j\)) in the former expression. For this reason, this is known as lowering an index. This effectively converts a vector (represented in coordinates) to a covector (represented in coordinates). This is why the "flat" notation is used (it is borrowed from musical notation, where a flat indicates the lowering of a tone). For this reason, the isomorphism \(\hat{g}\) is known as the musical isomorphism.

Note that, since the matrix is symmetric, many authors will write a transposed expression as follows:

\[v^{\flat} = \hat{g}(v) = g_{ij}v^i\varepsilon^j = v_j\varepsilon^j.\]

Likewise, using the same formula for the matrix representation as above, the inverse map \(\hat{g}^{-1} : V^* \rightarrow V\) can be represented as

\[\hat{g}^{-1}(\omega) = g^{ij}\omega_jE_i,\]

where \(g^{ij}\) is the matrix representation of \(\hat{g}^{-1}\). Note that, since \(\hat{g}\) and \(\hat{g}^{-1}\) are inverses, it follows that their respective matrices \(g_{ij}\) and \(g^{ij}\) are inverses.

Writing \(\omega^i = g^{ij}\omega_j\), we then obtain

\[\omega^{\sharp} = \hat{g}^{-1}(\omega) = g^{ij}\omega_jE_i = \omega^iE_i.\]

Likewise, since the subscript (\(j\)) was converted to a superscript (\(i\)), this is known as raising an index. This effectively converts a covector (represented in coordinates) to a vector (represented in coordinates). This is why the "sharp" notation is used (it is borrowed from musical notation, where a sharp indicates the raising of a tone).

Inner Products in Coordinates

Note that, since we determined that \(\hat{g}(v) = g_{ij}v^j\varepsilon^i\), it follows that

\[\hat{g}(v)(w) = g_{ij}v^j\varepsilon^i(w) = g_{ij}v^jw^i.\]

Thus, the general expression in coordinates for the action of an inner product on two vectors is

\[g(v,w) = g_{ij}v^jw^i\].

This is a generalization of the Euclidean dot product, in which case \(g_{ij} = \delta_{ij}\), i.e. the representing matrix is the identity matrix. Again, since the matrix \(g_{ij}\) is symmetric, this can be written as

\[g(v,w) = g_{ij}v^iw^j\].

This product can be expressed using matrix multiplication equivalently as

\[v^T G w\]

or

\[w^T G v,\]

where \(G\) is the matrix whose entries are \(g_{ij}\). In the case of the Euclidean dot product, \(G = I\), and this expression reduces to either \(w^Tv\) or \(v^Tw\), both of which are equal to \(v \cdot w = w \cdot v\).

Note also that, given any orthogonal basis \((\hat{E}_i)\), the matrix \(g_{ij}\) will necessarily be diagonal, since \(g_{ij} = g(\hat{E}_i,\hat{E}_j) = 0\) when \(i \neq j\). If the basis is orthonormal, then the matrix will be the identity matrix, since \(g_{ii} = g(\hat{E}_i,\hat{E}_j) = \lvert E_i \rvert = 1\) for all \(i\). Thus \(g_{ij} = \delta_{ij}\) whenever the chosen basis is orthonormal.

Given a basis \((E_1,\dots,E_n)\), we may also write inner products in terms of tensor products of the corresponding basis covectors \((\varepsilon^i,\dots,\varepsilon^j)\).

Since \(g(v,w) = g_{ij}v^jw^i = g_{ij}\varepsilon^j(v)\varepsilon^i(w) = g_{ij} \varepsilon^j \otimes \varepsilon^i(v, w)\), we may also write this as follows (re-arranging \(i\) and \(j\) since \(g\) is symmetric):

\[g = g_{ij}\varepsilon^i \otimes \varepsilon^j.\]

The tensor product \(\varepsilon^i \otimes \varepsilon^j\) is symmetric and thus coincides with the symmetric product \(\varepsilon^i\varepsilon^j\), so the following alternative notation is often used:

\[g = g_{ij}\varepsilon^i \varepsilon^j.\]

If the basis is orthonormal, then \(g_{ij}\) this may be written as

\[g = \delta_{ij}\varepsilon^i \varepsilon^j,\]

or, alternatively, using the notation \(\varepsilon^i\varepsilon^i = (\varepsilon^i)^2\), as

\[g = (\varepsilon^1)^2 + \dots + (\varepsilon^n)^2.\]

The dot product, then, may be written in the following form:

\[g = (e^1)^2 + \dots + (e^n)^2.\]

The positive definiteness of the inner product ensures that the signs are all positive (i.e. \(g_{ij} \geq 0\).

Scalar Product Spaces

Scalar product spaces represent an important generalization of inner product spaces. Recall that we previously established that the positive definiteness of an inner product induces the "musical" isomorphism between the underlying vector space \(V\) and its respective dual space \(V^*\). Given any symmetric, covariant \(2\)-tensor \(g\) on \(V\) (sometimes called a symmetric bilinear form), we say that \(g\) is non-degenerate if the induced linear map \(\hat{g} : V \rightarrow V^*\) defined by

\[\hat{g}(v)(w) = g(v,w)\]

is an isomorphism. Thus, every inner product is non-degenerate. A scalar product is a non-degenerate symmetric bilinear form on a vector space, and a scalar product space is a vector space equipped with a scalar product. Thus, a scalar product space is like an inner product space, except that the condition of positive definiteness is relaxed. Once positive definiteness is relaxed, we cannot infer the musical isomorphism, and must stipulate it as a condition instead.

The same notation and terminology is used for scalar product spaces as for inner product spaces. Thus, the scalar product of vectors \(v,w \in V\) in a vector space \(V\) is denoted \(\langle v,w \rangle\).

The norm of a vector \(v\) is defined to be

\[\lvert v \rvert = \lvert \langle v,v \rangle \rvert^{\frac{1}{2}},\]

that is, the square root of the absolute value of the scalar product of a vector with itself. This change is necessitated by the fact that the scalar product of a vector with itself may be negative. Note that the norm of a scalar product space does not necessarily satisfy the definition of a norm in a normed vector space, yet it is still customary to call it a "norm".

In particular, since a scalar product is not necessarily positive definite, the scalar product of a vector with itself can be \(0\).

The Gram-Schmidt procedure requires some modification. The "triangle completion" is instead calculated as

\[v - \langle u,u \rangle \langle v,u \rangle u,\]

which is orthogonal to \(u\) as can be confirmed as follows:

\begin{align}\langle u, v - \langle u,u \rangle \langle v,u \rangle u \rangle &= \langle u, v \rangle - \langle u, \langle u,u \rangle \langle v,u \rangle u \rangle\\&= \langle u,v \rangle - \langle v,u \rangle \langle u,u \rangle \langle u,u \rangle \\&= \langle u,v \rangle - \langle v,u \rangle \\&= \langle u,v \rangle - \langle u,v \rangle \\&= 0.\end{align}

The extra term of \(\langle u,u \rangle\) ensures that the signs are correct.

A non-degenerate subspace \(S\) of a vector space \(V\) is a subspace such that the restriction of a scalar product \(g\) to \(S\) is non-degenerate. An ordered tuple \((v_1,\dots,v_k)\) of \(k\) vectors is non-degenerate if the vectors \((v_1,\dots,v_j)\) span a non-degenerate \(j\)-dimensional subspace for every \(j=1,\dots,k\).

Given a non-degenerate basis \((E_i)\) for a scalar product space \((V,g)\), we can produce an orthonormal basis using a modified version of the Gram-Schmidt procedure.

We first define

\[\hat{E}_1 = \frac{E_1}{\lvert E_1 \rvert}.\]

Since the basis \((E_i)\) is non-degenerate, the subspace \(S_1\) spanned by \(E_1\) is non-degenerate. This means that there exists a non-zero vector \(s \in S_1\) such that \(g(E_1, s) \neq 0\). Since \(E_1\) spans \(S_1\), \(s = aE_1\) for some \(a \in \mathbb{R}\), and thus \(g(E_1, s) = g(E_1, aE_1) = ag(E_1,E_1)\) and thus, since \(a \neq 0\), it follows that \(g(E_1,E_1) \neq 0\). This means that \(\lvert E_1 \rvert \neq 0\) and the denominator is non-zero.

The inductive step then computes a new vector defined as

\[z_k = E_k - \sum_{i=1}^{k-1} \langle \hat{E}_i, \hat{E}_i \rangle \langle E_k, \hat{E}_i \rangle \hat{E}_i.\]

Then set

\[\hat{E}_k = \frac{z_k}{\lvert z_k \rvert}.\]

Now, by construction, \(\mathrm{span}(E_1,\dots,E_k) = \mathrm{span}(\hat{E}_1,\dots,\hat{E}_{k-1},z_k)\). Since the basis \((E_i)\) is non-degenerate, the subspace \(S_k\) spanned by \((E_1,\dots,E_k)\) is non-degenerate. This means that, for each element \(s \in S_k\), there exists some element \(t \in S_k\) such that \(g(s, t) \neq 0\). If \(t = t^iE_i\) in terms of \(S_k\), then \(g(s,t) = g(s, t^iE_i) = t^ig(s, E_i)\) and thus \(t^ig(s, E_i) \neq 0\). Thus, since \(s \in S_k\), it follows that \(s\) cannot be orthogonal to all of the \(E_i\), since otherwise \(g(s, E_i) = 0\) and \(g(s,t) = 0\). Thus, if some non-zero vector \(v \in V\) is orthogonal to every element of \(S_k\), then, in particular \(g(v, E_i) = 0\) for all \(E_i\) and thus \(v \not \in S_k\). Now, if \(g(z_k,z_k) = 0\), then, since \(g(z_k, \hat{E}_i) = 0\) by construction for all \(i \in (1,\dots,k-1)\), then \(z_k\) is orthogonal to the spanning set \((\hat{E}_1,\dots,\hat{E}_{k-1},z_k)\) and thus orthogonal to all vectors in \(S_k\) as well, which contradicts the assumption of non-degeneracy. Thus, \(g(z_k,z_k) \neq 0\) and \(\lvert z_k \rvert \neq 0\). The denominator is therefore non-zero.

The definition of orthogonal vectors and angles is the same.

Likewise, a scalar product \(g\) can be represented in coordinates. However, since \(g\) is not necessarily positive definite, the representing matrix \(g_{ij}\) relative to a chosen basis might contain negative entries. In the case of an orthogonal basis, we can likewise infer that the matrix \(g_{ij}\) will be diagonal. However, some of the entries may still be negative since the inner product of this basis vector with itself can be negative.

Thus, arranging the negative terms last for convenience, the general expression in coordinates for a scalar product on a vector space \(V\) in terms of a the dual basis \((\varepsilon^i)\) corresponding to a chosen orthonormal basis \((\hat{E}_i)\) is

\[g = (\varepsilon^1)^2 + \dots + (\varepsilon^r)^2 - (\varepsilon^{r+1})^2 - \dots - (\varepsilon^{r+s})^2,\]

where \(\mathrm{dim}(V) = n\), \(n = r + s\), \(r\) is the number of positive coefficients, and \(s\) is the number of negative coefficients. The tuple \((r,s)\) is called the signature of the scalar product.

The theorem of linear algebra known as Sylvester's Law of Inertia implies that the signature does not depend on the chosen basis and is therefore an invariant of the scalar product space, and we may thus speak of "the" signature since it is unique.

Metric Tensors

As previously indicated, inner products and scalar products on a vector space \(V\) are tensors (bilinear maps with signature \(V \times V \rightarrow \mathbb{R}\). Each is additionally a symmetric tensor. Inner products are positive definite, whereas scalar products are simply non-degenerate. Generically, we may call such tensors metric tensors or just metrics. However, note that the terms "metric" and "metric tensor" are overloaded. Such a metric is not the same as a metric in the sense of a metric space. Often, metric tensor fields and metric tensors are both called "metrics" or "metric tensors"; context will indicate which is intended. Usually, in the context of smooth manifolds, "metric" refers to a metric tensor field.

Metric Tensor Fields

On a smooth manifold, we desire to have a metric tensor that varies smoothly from point to point. That is, at each point \(p\), we want a metric tensor \(g_p\). In other words, we want a smooth tensor field.

There are two primary cases of interest for a smooth manifold \(M\):

• A Riemannian metric on \(M\) is a smooth, symmetric, covariant \(2\)-tensor field on \(M\) that is positive definite at each point. A Riemannian manifold is a smooth manifold \(M\) together with a Riemannian metric \(g\).
• A semi-Riemannian metric (or pseudo-Riemannian metric) on \(M\) is a smooth, symmetric, covariant \(2\)-tensor field on \(M\) that is non-degenerate at each point. A semi-Riemannian manifold (or pseudo-Riemannian manifold) is a smooth manifold \(M\) together with a pseudo-Riemannian metric \(g\).

Thus, Riemannian metrics define an inner product \(g_p\) on each tangent space \(T_pM\), and semi-Riemannian metrics define a scalar product \(g_p\) on each tangent space \(T_pM\). Often, notation such as \(\langle v, w \rangle_g\) or \(\langle v,w \rangle_p\) will be used to indicate \(g_p(v,w)\) for \(v,w \in T_pM\).

Riemannian metrics have many applications in mathematics, and semi-Riemannian metrics are important because of their applications in physics, particularly in general relativity.

Each of the facts established for inner or scalar products can now be extended to metric tensor fields.

Given any frame \((E_1, \dots, E_n)\) for an \(n\)-dimensional smooth manifold \(M\) with dual co-frame \((\varepsilon^1, \dots, \varepsilon^n)\), we can write \(g\) as

\[g = g_{ij}\varepsilon^i \otimes \varepsilon^j,\]

where

\[g_{ij} = g(E_i, E_j).\]

Thus, \(g_{ij}\) is a collection of functions (which can be organized as a matrix of functions) which assigns a scalar coefficient to each point \(p\), and thus

\[g_p = g_{ij}(p)\varepsilon^i\rvert_p \otimes \varepsilon^j\rvert_p\]

and

\[g_{ij}(p) = g_p(E_i\rvert_p, E_i\rvert_p).\]

Since \(g\) is a symmetric tensor field, we can write it in terms of symmetric products also:

\begin{align}g &= g_{ij}\varepsilon^i \otimes \varepsilon^j \\&= \frac{1}{2}\left(g_{ij}\varepsilon^i \otimes \varepsilon^j + g_{ij}\varepsilon^i \otimes \varepsilon^j \right) \\&= \frac{1}{2}\left(g_{ij}\varepsilon^i \otimes \varepsilon^j + g_{ji}\varepsilon^i \otimes \varepsilon^j \right) & \text{(Since \(g_{ij} = g_{ji}\))} \\&= \frac{1}{2}\left(g_{ij}\varepsilon^i \otimes \varepsilon^j + g_{ij}\varepsilon^j \otimes \varepsilon^i \right) & \text{(Swap indices \(i\) and \(j\))} \\&= g_{ij}\frac{1}{2}\left(\varepsilon^i \otimes \varepsilon^j + \varepsilon^j \otimes \varepsilon^i \right) \\&= g_{ij}\varepsilon^i\varepsilon^j .\end{align}

Thus, we may also write

\[g = g_{ij}\varepsilon^i\varepsilon^j.\]

In particular, given smooth local coordinates \((x^i)\), we may write \(g\) in terms of the corresponding coordinate frame \((\partial/\partial x^i)\) and dual frame \((dx^i)\):

\[g = g_{ij} dx^i \otimes dx^j = g_{ij} dx^idx^j,\]

where

\[g_{ij} = g\left(\frac{\partial}{\partial x^i}, \frac{\partial}{\partial x^j}\right)\]

and thus

\[g_{ij}(p) = g_p\left(\frac{\partial}{\partial x^i}\bigg\rvert_p, \frac{\partial}{\partial x^j}\bigg\rvert_p\right)\]

and

\[g_p = g_{ij}(p) dx^i\rvert_pdx^j\rvert_p.\]

A frame \((E_i)\) is an orthonormal frame with respect to \(g\) whenever \(g(E_i, E_j) = \delta_{ij}\), where \(\delta_{ij}\) is a collection of constant functions defined such that

\[\delta_{ij}(p) = \begin{cases}1 & \text{if \(i = j\)},\\0 &\text{otherwise}.\end{cases}\]

Thus, the coordinate expression for \(g\) is simplified to

\[g = g_{ij}\varepsilon^i\varepsilon^j = g(E_i, E_j)\varepsilon^i\varepsilon^j = \delta_{ij}\varepsilon^i\varepsilon^j.\]

Using the notational abbreviation \(\varepsilon^i\varepsilon^i = (\varepsilon^i)^2\), this can also be written as follows:

\[g = (\varepsilon^1)^2 + \dots + (\varepsilon^n)^2.\]

In particular, on the manifold \(\mathbb{R}^n\), the standard coordinate frame \((x^i)\) (i.e. the projection that selects the \(i\)-th component of each tuple) is an orthonormal frame with respect to the tensor field \(g_p(v,w) = v \cdot w\) (called the Euclidean metric).

Recall that, for any tangent vector \(v \in T_p\mathbb{R}^n\) (i.e. a derivation at the point \(p\)), under the isomorphism \(T_p\mathbb{R}^n \cong \mathbb{R}^n\) (witnessed by \(v \rightarrow v(x^i)E_i\) with inverse \(v^iE_i \rightarrow v^i \partial/\partial x^i \rvert_p\)), we can define

\[v \cdot w = \sum_{i=1}^n v(x^i) w(x^i) = \sum_{i=1}^n v^i w^i.\]

Then, for any coordinate vector \(\partial/\partial x^j\),

\[\frac{\partial}{\partial x^j}\bigg\rvert_p(x^i) = \frac{\partial x^i}{\partial x^j}(p) = \delta_{ij}.\]

Thus, the coordinate frame is an orthonormal frame with respect to the Euclidean metric.

This yields

\[g = \delta_{ij}dx^idx^j\]

and thus

\[g = (dx^1)^2 + \dots + (dx^n)^2.\]

We can confirm that this represents the Euclidean dot product:

\[g_p(v, w) = \delta_{ij}dx^idx^j(v,w) = \delta_{ij}v^iv^j = \sum_{i=1}^n v^iw^i = v \cdot w.\]

Smooth coordinate frames are not, in general, orthonormal frames; however, the standard coordinate frame on \(\mathbb{R}^n\) is an orthonormal frame with respect to the Euclidean metric.

The Gram-Schmidt algorithm can be applied point-wise to create an orthonormal frame from any frame.

Pullback Metrics

Recall that the pullback \(F^*A\) of a covariant \(k\)-tensor field \(A\) defined on a smooth manifold \(N\) along a smooth map \(F : M \rightarrow N\) between a smooth manifold \(M\) and \(N\) is defined, for each \(p \in M\), and vectors \(v_1,\dots,v_k \in T_pM\) as follows:

\[(F^*A)_p(v_1,\dots,v_k) = A_{F(p)}\left(dF_p(v_1),\dots,dF_p(v_k)\right).\]

Thus, in particular, the pullback \(F^*g\) of a metric tensor \(g\) defined on a smooth manifold \(N\) is defined as follows for any vectors \(v,w \in T_pM\)

\[(F^*g)_p(v, w) = g_{F(p)}\left(dF_p(v),\dots,dF_p(w)\right).\]

Since \(g\) is symmetric, the pullback is also symmetric, since

\begin{align}(F^*g)_p(v, w) &= g_{F(p)}\left(dF_p(v),dF_p(w)\right) \\&= g_{F(p)}\left(dF_p(w),dF_p(v)\right) \\&= (F^*g)_p(w, v).\end{align}

Thus, if \(F^*g\) is also positive definite, then it is a Riemannian metric, and if \(F^*g\) is also non-degenerate, it is a semi-Riemannian metric.

If \(F\) is a smooth immersion, then, by definition, the differential \(dF_p : T_pM \rightarrow T_{F(p)}N\) at each point \(p \in M\) is injective, and, since \(dF_p\) is a linear map, it maps the zero vector of \(T_pM\) to the zero vector of \(T_{F(p)}\) and hence maps no other vector in \(T_pM\) to the zero vector of \(T_{F(p)}N\). This means that \(dF_p(v) = 0 \) if and only if \(v = 0\). Thus, if \(g\) is positive definite, then so is \(F^*g\).

Likewise, if \(g\) is non-degenerate, then each map \(\widehat{F^*g}_p(v) : T_pM \rightarrow T^*_pM\) defined as

\[\widehat{F^*g}_p(v)(w) = F^*g(v, w) = g_{F(p)}(dF_p(v), dF_p(w)) = \hat{g}_{F(p)}(dF_p(v))(dF_p(w))\]

has the trivial kernel \(\{0\}\) and hence is an isomorphism, which means that \(F^*g\) is non-degenerate. To see this, note that, if \(\widehat{F^*g}_p(v) = 0\), then \(\hat{g}_{F(p)}(dF_p(v)) = 0\), and so, since \(\hat{g}_{F(p)}\) is an isomorphism, \(dF_p(v) = 0\), and since \(dF_p\) is and injective linear map, \(v = 0\).

Thus, for any smooth immersion \(F\), if \(g\) is semi-Riemannian, then \(F^*g\) is semi-Riemannian, and if \(g\) is Riemannian, then \(F^*g\) is Riemannian.

Example

As an example of a pullback metric, consider the Euclidean metric \(g = dx^2 + dy^2\) on \(\mathbb{R}^2\) and the map \(F : \mathbb{R}^2 \rightarrow \mathbb{R}^2\) representing polar coordinates defined as

\[F(r, \theta) = (r \cos \theta, r \sin \theta).\]

Recall that, to compute the pullback of a tensor field, we may substitute \(x = r \cos \theta\) and \(y = \r \sin \theta) and expand as follows:

\begin{align}g &= dx^2 + dy^2 \\&= d(r \cos \theta)^2 + d(r \sin \theta)^2 \\&= (\cos \theta dr - r \sin \theta d\theta)^2 + (\sin \theta dr + r \cos \theta d\theta)^2 \\&= \cos^2 \theta dr^2 - 2 r \cos \theta \sin \theta dr d\theta + r^2 \sin^2 \theta d\theta^2 + \sin^2 \theta dr^2 + 2r \cos \theta \sin \theta dr d\theta + r^2 \cos ^2 \theta d\theta^2 \\&=(\cos^2 \theta + \sin^2\theta) dr^2 + (r^2 \sin^2\theta + r^2\cos^2\theta)d\theta^2 \\&= dr^2 + r^2d\theta^2. \end{align}

Isometries

Pullback metrics provide a means of extending the notion of an isometry of inner product (or scalar product) spaces to smooth manifolds. If \((M,g)\) and \((N,\tilde{g})\) are smooth manifolds (whether semi-Riemannian or Riemannian), then a smooth map \(F : M \rightarrow N\) is called an isometry if it is a diffeomorphism and \(F^*\tilde{g} = g\). At each point \(p \in M\), the map \(dF_p : T_pM \rightarrow T_{F(p)}N\) represents the best linear approximation of \(F\) at the point \(p\), and thus the condition that \(F^*\tilde{g} = g\) is means that \(dF_p\) is an isometry of inner product or scalar product spaces since, by definition, \(\tilde{g}_{F(p)}(dF_p(v),dF_p(w)) = g(v,w)\) for all \(v,w \in T_pM\).

A local isometry is a map \(F\) as above where \(F^*\tilde{g} = g\) which is instead a local diffeomorphism.

If two manifolds admit a (global or local) isometry, they are called (globally or locally) isometric.

Musical Isomorphism

Given a metric \(g\), the isomorphism between tangent spaces and cotangent spaces induced by \(g_p\) can be extended to an isomorphism between the tangent and cotangent bundles.

For any (Riemannian or semi-Riemannian) metric \(g\) on a smooth manifold \(M\), define a map \(\hat{g} : TM \rightarrow T^*M\) as follows for each \(p \in M \) and \(v,w \in T_pM\):

\[\hat{g}(v)(w) = g_p(v, w).\]

This map likewise acts on vector fields \(X, Y \in \mathfrak{X}(M)\) as follows:

\[\hat{g}(X)(Y) = g(X,Y).\]

Given smooth coordinates \((x^i)\), the tensor field \(g\) can be written as

\[g = g_{ij}dx^idx^j.\]

Next, consider the action of \(\hat{g}\) on vector fields \(X,Y\) in these coordinates:

\begin{align}\hat{g}(X)(Y) &= g(X,Y) \\&= g_{ij}dx^idx^j(X, Y) \\&= g_{ij}dx^i(X)dx^j(Y) \\&= g_{ij}X^iY^j.\end{align}

This implies that

\[\hat{g}(X) = g_{ij}X^idx^j,\]

since then

\[\hat{g}(X)(Y) = g_{ij}X^idx^j(Y) = g_{ij}X^iY^j.\]

The components of the covector field \(\hat{g}(X)\) are often denoted as

\[\hat{g}(X) = X_jdx^j,\]

which then implies that

\[X_j = g_{ij}X^i.\]

Another way to compute the components is to apply \(\hat{g}(X)\) to the coordinate vector fields \(\partial/\partial x^j\):

\begin{align}X_j = \hat{g}(X)\left(\frac{\partial}{\partial x^j}\right) &= g_{ij}dx^i(X)dx^j\left(\frac{\partial}{\partial x^j}\right) \\&= g_{ij}X^i.\end{align}

Thus, the vector field \(X\) is written as

\[X = X^i \frac{\partial}{\partial x^i}\]

and the corresponding covector field \(\hat{g}(X)\) is written as

\[\hat{g}(X) = X_j dx^j.\]

For this reason, one often says that the covector field \(\hat{g}(X)\) is obtained from the vector field \(X\) by lowering an index (i.e. the index \(i\) is a superscript in the expression \(X^i \frac{\partial}{x^i}\) and it was "lowered" to a subscript \(j\) in the expression \(X_j dx^j\)). Notice that the \(i\) was changed to a \(j\) and the coordinate vector field \(\partial/\partial x^j\) was changed to a coordinate covector field \(dx^j\) also.

The notation

\[X^{\flat} = \hat{g}(X)\]

is often used because the "flat" symbol \(\flat\) is used in musical notation to indicate the lowering of a tone. For this reason, the isomorphism between the tangent and cotangent bundles is often referred to as the musical isomorphism.

Since \(\hat{g}\) is an isomorphism, there exists an inverse \(\hat{g}^{-1} : T^*_pM \rightarrow T_pM\). Since \(g_{ij}\) is the matrix representation of the map \(\hat{g}\) in the given coordinates, there likewise exists an inverse matrix which represents \(\hat{g}^{-1}\) in these coordinates which we denote as \(g^{ij}\).

Thus, as with the matrix representation of any linear map, if an element of \(\omega \in T^*_pM\) has representation \(\omega_j dx^j\), then, we can multiply by the matrix \(g^{ij}\) and obtain its representation in \(T_pM\) as follows:

\[\hat{g}^{-1}(\omega) = \omega^i \frac{\partial}{\partial x^i},\]

where

\[\omega^i = g^{ij}\omega_j.\]

Thus, we likewise say that \(\hat{g}^{-1}(\omega)\) is obtained from \(\omega\) by raising an index, and we use the notation \(\omega^{\sharp} = \hat{g}^{-1}(\omega)\) (which likewise comes from musical notation).

Gradients

One important application of the sharp operation is related to the gradient of a smooth function \(f : M \rightarrow \mathbb{R}\) defined on a manifold \(M\) endowed with a (Riemannian or semi-Riemannian) metric \(g\). The gradient of \(f\) is defined to be the vector field

\[\mathrm{grad} f = (df)^{\sharp} = \hat{g}^{-1}(df).\]

Applying the definition, we see that, for any vector field \(X \in \mathfrak{M}\),

\begin{align}g(\mathrm{grad} f, X) &= \hat{g}(\mathrm{grad} f)(X) \\&= \hat{g}(\hat{g}^{-1}(df)(X) \\&= df(X) \\&= Xf.\end{align}

Thus, \(\mathrm{grad} f\) is the unique vector field which satisfies

\[g(\mathrm{grad} f, -) = df.\]

In other words, the gradient \(\mathrm{grad} f\) is the representation of the (global) differential \(df\) (which is a covector field) as a vector field relative to the metric \(g\).

The differential is expressed in coordinates as follows:

\[(df)_i = df\left(\frac{\partial}{\partial x^i}\right) = \frac{\partial f}{\partial x^i}.\]

Thus, the gradient may be expressed in coordinates, just as any covector field may be expressed in coordinates, as

\[\mathrm{grad} f = g^{ij}(df)_i \frac{\partial}{\partial x^j} = g^{ij}\frac{\partial f}{\partial x^i} \frac{\partial}{\partial x^j}.\]

Under the Euclidean metric on \(\mathbb{R}^n\), since the metric has representation \(\delta^{ij}\), the gradient is expressed as

\[\mathrm{grad} f = \delta^{ij}\frac{\partial f}{\partial x^i} \frac{\partial}{\partial x^j} = \sum_{i=1}^n \frac{\partial f}{\partial x^i} \frac{\partial}{\partial x^i}.\]

Using the isomorphism \(T_p\mathbb{R}^n \cong \mathbb{R}\), the gradient can further be expressed in terms of the standard basis \((e^i)\) as

\[\mathrm{grad}~f = \frac{\partial f}{\partial x^i}e^i = (\frac{\partial f}{\partial x^1},\dots,\frac{\partial f}{\partial x^n}).\]

Thus, we can recover the classical definition of the gradient from calculus using the definition of a gradient on a general manifold. This is how the gradient is sometimes introduced in elementary calculus, namely, as a tuple of partial derivatives.

Volume Forms

A metric also permits us to define volumes (i.e. lengths, areas, volumes, and higher-dimensional generalizations) on manifolds.

We typically think of such measurements in terms of orthonormal bases. For instance, the unit cube (the cube of volume \(1\)) in \(\mathbb{R}^3\) is spanned by the three orthonormal basis vectors \((e^1, e^2, e^3\). It is with respect to an orthonormal basis that we make standard measurements of volumes. Such volumes are also oriented.

Thus, for any oriented smooth \(n\)-dimensional Riemannian manifold \(M\) equipped with a metric \(g\), we define the volume form to be the unique smooth orientation form \(\omega_g \in \Omega^n(M)\) which, for every local oriented orthonormal frame \((E_1,\dots,E_n)\) relative to \(g\) on \(M\), satisfies the relation

\[\omega_g(E_1,\dots,E_n) = 1.\]

Now, if \((E_1,\dots,E_n)\) is any local oriented orthonormal frame defined on an open subset \(U \subseteq M\) and \((\varepsilon^1,\dots,\varepsilon^n)\) is its corresponding dual coframe, then, since \(\omega_g\) is a top-level form, it can be represented in terms of the dual coframe as

\[\omega_g = \omega_g(E_1,\dots,E_n) \varepsilon^1 \wedge \dots \wedge \varepsilon^n = \varepsilon^1 \wedge \dots \wedge \varepsilon^n.\]

Thus, given a coordinate frame, the form of \(\omega_g\) in terms of this frame is uniquely determined. If \((\tilde{E}_1,\dots,\tilde{E}_n)\) is another local oriented orthonormal frame defined on \(U\) with dual coframe \((\tilde{\varepsilon}_1,\dots,\tilde{\varepsilon}_n)\), then we can then likewise define

\[\tilde{\omega}_g = \tilde{\varepsilon}_1 \wedge \dots \wedge \tilde{\varepsilon}_n.\]

We can write \((A^j_i)\) for the transition matrix (i.e. a matrix of smooth functions), so that, by definition,

\[\tilde{E}_i = A^j_iE_j.\]

Since both frames are orthonormal and consistently oriented means that \(\mathrm{det}(A^j_i) = 1\). We can then compute

\begin{align}\omega_g(\tilde{E}_1,\dots,\tilde{E}_n) &= \varepsilon^1 \wedge \dots \wedge \varepsilon^n(\tilde{E}_1,\dots,\tilde{E}_n) \\&= \mathrm{det}(\varepsilon^j)(\tilde{E}_i)) \\&= \mathrm{det}(\varepsilon^j)(A^j_iE_j)) \\&= \mathrm{det}(A^j_i \varepsilon^j)(E_j)) \\&= \mathrm{det}(A^j_i) \\&= 1 = \tilde{\omega}_g(\tilde{E}_1,\dots,\tilde{E}_n).\end{align}

Thus, \(\omega_g = \tilde{\omega}_g\). Thus, the volume form is uniquely determined and independent of the choice of local oriented orthonormal frame.

If \((M,g)\) and \((\tilde{M},\tilde{g})\) are manifolds with metrics and \(F : M \rightarrow \tilde{M}\) is a local diffeomorphism, then, for any local oriented frame \((\tilde{E}_i)\) on \(\tilde{M}\) that is orthonormal relative to \(\tilde{g}\), we can compute

\begin{align}F^*\omega_{\tilde{g}}\left(dF^{-1}(\tilde{E}_1),\dots,dF^{-1}(\tilde{E}_n)\right) &= \omega_{\tilde{g}}\left(dF\left(dF^{-1}(\tilde{E}_1)\right),\dots,dF\left(dF^{-1}(\tilde{E}_n)\right)\right) \\&= \omega_{\tilde{g}}(\tilde{E}_1,\dots,\tilde{E}_n) \\&= 1.\end{align}

Likewise, for any pair \(\tilde{E}_i,\tilde{E}_j\), we compute

\begin{align}F^*\tilde{g}\left(dF^{-1}(\tilde{E}_i),dF^{-1}(\tilde{E}_j)\right) &= \tilde{g}\left(dF\left(dF^{-1}(\tilde{E}_i)\right),dF\left(dF^{-1}(\tilde{E}_j)\right)\right) \\&= \tilde{g}(\tilde{E}_i,\tilde{E}_j) \\&= \delta_{ij}.\end{align}

Thus, the frame \(\left(dF^{-1}(\tilde{E}_1),\dots,dF^{-1}(\tilde{E}_n)\right)\) is orthonormal with respect to \(F^*\tilde{g}\). Since \(dF^{-1}\) is an isomorphism (and thus surjective), every local oriented frame on \(M\) has the form \(\left(dF^{-1}(\tilde{E}_1),\dots,dF^{-1}(\tilde{E}_n)\right)\) for some frame \((\tilde{E}_i)\) on \(\tilde{M}\) (including those that are orthonormal relative to \(g\)), and thus \(F^*\omega_{\tilde{g}}\) is a volume form on \((M,(F^*\tilde{g}))\). If \(F\) is an isometry, \(F^*\tilde{g} = g\), and thus \(F^*\omega_{\tilde{g}}\) is a volume form on \((M,g)\), and, since volume forms are unique, it follows that

\[F^*\omega_{\tilde{g}} = \omega_g.\]

It is useful to consider the expression for a volume form in coordinates. Given a smooth \(n\)-dimensional manifold \(M\) equipped with a metric \(g\) and a smooth oriented orthonormal frame \((E_i)\) with dual coframe \((\varepsilon^i)\), we may write the coordinate frame in terms of the orthonormal frame as

\[\frac{\partial}{\partial x^i} = A^j_i E_j\]

for some matrix of smooth functions \((A^j_i)\).

The volume form \(\omega_g\), like every \(n\)-form on \(M\), may be expressed as

\[\omega_g = f dx^1 \wedge \dots \wedge dx^n\]

for some smooth function \(f\). We can compute \(f\) by computing the coordinate expression for \(\omega_g\), which, as for any tensor field, is computed as

\begin{align}f &= \omega_g\left(\frac{\partial}{\partial x^1},\dots,\frac{\partial}{\partial x^n}\right) \\&= \varepsilon^1 \wedge \dots \wedge \varepsilon^n\left(\frac{\partial}{\partial x^1},\dots,\frac{\partial}{\partial x^n}\right) \\&= \mathrm{det}\left(\varepsilon^j\left(\frac{\partial}{\partial x^i}\right)\right) \\&= \mathrm{det}(\varepsilon^j(A^j_i E_j)) \\&= \mathrm{det}(A^j_i \varepsilon^j( E_j)) \\&= \mathrm{det}(A^j_i).\end{align}

Likewise, we can compute the coordinates of \(g\) in terms of the coordinate basis as

\begin{align}g_{ij} &= g\left(\frac{\partial}{\partial x^i},\frac{\partial}{\partial x^j}\right) \\&= g(A^k_i E_k, A^l_j E_l) \\&= A^k_i A^l_j g( E_k, E_l) \\&= A^k_i A^l_j \delta_{kl} \\&= \sum_k A^k_i A^k_j = A^TA.\end{align}

Thus, we have

\begin{align}\mathrm{det}(g_{ij}) &= \mathrm{det}(A^TA) \\&= \mathrm{det}(A^T)\mathrm{det}(A) \\&= \mathrm{det}(A)\mathrm{det}(A) \\&= (\mathrm{det}(A))^2.\end{align}

Thus

\[\sqrt{\mathrm{det}(g_{ij})} = \sqrt{(\mathrm{det}(A))^2} = \lvert \mathrm{det} A \rvert,\]

and thus

\[\mathrm{det}(A) = \pm \sqrt{\mathrm{det}(g_{ij})}.\]

Since both \((E_i)\) and \((\partial/\partial x^i)\) are oriented, the sign is positive, and so \(f = \sqrt{\mathrm{det}(g_{ij})}\), and

\[\omega_g = \sqrt{\mathrm{det}(g_{ij})} ~dx^1 \wedge \dots \wedge dx^n.\]

Arc Length

One important application of Riemannian metrics is the calculation of the arc length of curves on smooth manifolds.

If \(M\) is a smooth manifold endowed with a Riemannian metric \(g\) and \(\gamma : [a, b] \rightarrow M\) is a piecewise smooth curve segment, the length of \(\mathbf{\gamma}\) is defined as follows:

\[L_g(\gamma) = \int_a^b \lvert \gamma'(t) \rvert_g ~dt.\]

Recall that the notation \(\gamma'(t_0)\) denotes the velocity of the curve \(\gamma\) and is defined as follows:

\[\gamma'(t_0) = d\gamma\left(\frac{d}{dt}\bigg\rvert_{t_0}\right) \in T_{\gamma(t_0)}M.\]

This definition of arc length is a straightforward extension of the classical notion of the arc length of a curve \(r : [a,b] \rightarrow \mathbb{R}^n\) in \(\mathbb{R}^n\), which is defined as

\[\int_a^b \lVert r'(t) \rVert ~dt,\]

where \(\lVert r'(t) \rVert\) denotes the Euclidean norm. Thus, the classical formula is modified to use an arbitrary metric instead of the Euclidean metric.

This can be thought of as the rectification of the curve into arbitrarily small line segments, whose norms are computed and combined in an integral.

Given smooth coordinates \((x^i)\) on \(M\), since \(g = g_{ij}dx^idx^j\) in terms of these coordinates, we can likewise compute

\begin{align}L_g(\gamma) &= \int_a^b \lvert \gamma'(t_0) \rvert_g ~dt_0 \\&= \int_a^b \sqrt{g_{\gamma(t_0)}(\gamma'(t_0), \gamma'(t_0))}~dt_0 \\&= \int_a^b \sqrt{g_{ij}(\gamma(t_0))dx^i\rvert_{\gamma(t_0)}dx^j\rvert_{\gamma(t_0)}(\gamma'(t_0), \gamma'(t_0))} ~dt_0 \\&= \int_a^b \sqrt{g_{ij}(\gamma(t_0))dx^i\rvert_{\gamma(t_0)}(\gamma'(t_0))dx^j\rvert_{\gamma(t_0)}(\gamma'(t_0))} ~dt_0 \\&= \int_a^b \sqrt{g_{ij}(\gamma(t_0))dx^i\rvert_{\gamma(t_0)}\left(d\gamma\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)dx^j\rvert_{\gamma(t_0)}\left(d\gamma\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)} ~dt_0 \\&= \int_a^b \sqrt{g_{ij}(\gamma(t_0))\left(\frac{d}{dt}\bigg\rvert_{t_0}(x^i \circ \gamma)\right)\left(\frac{d}{dt}\bigg\rvert_{t_0}(x^j \circ \gamma)\right)} ~dt_0 \\&= \int_a^b \sqrt{g_{ij}(\gamma(t_0))(\dot{\gamma}^i(t_0))(\dot{\gamma}^j(t_0))} ~dt_0.\end{align}

Thus, in the Euclidean metric \(g = \delta_{ij}dx^idx^j\) on \(\mathbb{R}^n\), this amounts to

\[\int_a^b \sqrt{(\dot{\gamma}^1(t_0))^2 + \dots + (\dot{\gamma}^n(t_0))^2} ~dt_0,\]

and thus the integrand is precisely the Euclidean norm of the vector consisting of the components of the curve, i.e. \((\dot{\gamma}^1(t_0),\dots,\dot{\gamma}^n(t_0))\).

This is also equivalent to computing the integral of the volume form of the pullback metric \(\gamma^*g\), whose matrix has only one entry \(\gamma^*g(d/dt\rvert_{t_0}, d/dt\rvert_{t_0})\), as the following calculation shows:

\begin{align}\int_a^b \sqrt{\mathrm{det}((\gamma^*g)_{t_0})} ~dt_0 &= \int_a^b \sqrt{\gamma^*g\left(\frac{d}{dt}\bigg\rvert_{t_0}, \frac{d}{dt}\bigg\rvert_{t_0}\right)}~dt_0 \\&= \int_a^b \sqrt{g_{\gamma(t_0)}\left(d\gamma\left(\frac{d}{dt}\bigg\rvert_{t_0}\right),d\gamma\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)}~dt_0 \\&= \int_a^b \sqrt{g_{\gamma(t_0)}(\gamma'(t_0),\gamma'(t_0))}~dt_0 \\&=\int_a^b \lvert \gamma'(t_0) \rvert_g~dt_0 .\end{align}

The length of a curve is a local isometry invariant of a Riemannian manifold, that is, if \((M,g)\) and \((\tilde{M},\tilde{g})\) are Riemannian manifolds and \(F : M \rightarrow \tilde{M}\) is a local isometry, then \(L_{\tilde{g}}(F \circ \gamma) = L_g(\gamma)\) for every piecewise smooth curve segment \(\gamma : [a,b] \rightarrow M\) in \(M\), as the following calculation demonstrates:

\begin{align}L_{\tilde{g}}(F \circ \gamma) &= \int_a^b \lvert (F \circ \gamma)'(t_0)\rvert_{\tilde{g}}~dt_0 \\&= \int_a^b \tilde{g}_{F(\gamma(t_0))}\left(d(F \circ \gamma)_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right),d(F \circ \gamma)_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)~dt_0 \\&= \int_a^b \tilde{g}_{F(\gamma(t_0))}\left(dF_{\gamma(t_0)}\left(d\gamma_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right),dF_{\gamma(t_0)}\left(d\gamma_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)\right)~dt_0 \\&= \int_a^b \tilde{g}_{F(\gamma(t_0))}(dF_{\gamma'(t_0)}(\gamma'(t_0)),dF_{\gamma'(t_0)}(\gamma'(t_0)))~dt_0 \\&= \int_a^b (F^*\tilde{\gamma})_{\gamma(t_0)}(\gamma'(t_0), \gamma'(t_0))~dt_0 \\&= \int_a^b g_{\gamma(t_0)}(\gamma'(t_0), \gamma'(t_0))~dt_0 \\&= \int_a^b \lvert \gamma'(t_0)\rvert_g~dt_0 \\&= L_g(\gamma).\end{align}

The length of a curve is also independent of the parametrization. A re-parametrization of a piecewise smooth curve segment \(\gamma : [a,b] \rightarrow M\) is a curve segment \(\tilde{\gamma} = \gamma \circ \varphi\) for some diffeomorphism \(\varphi : [c,d] \rightarrow [a,b]\). Consider the following calculation:

\begin{align}L_g(\tilde{\gamma}) &= \int_c^d \lvert \tilde{\gamma}'(t_0) \rvert_g~dt_0 \\&= \int_c^d \bigg\lvert d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\bigg\rvert_g~dt_0 \\&= \int_c^d \sqrt{g_{\tilde{\gamma}(t_0)}\left(d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right), d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\tilde{\gamma}(t_0))dx^idx^j\left(d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right), d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\tilde{\gamma}(t_0))dx^i\left(d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)dx^j\left(d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\tilde{\gamma}(t_0))\left(d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)(x^i)\right)\left(d\tilde{\gamma}_{t_0}\left(\frac{d}{dt}\bigg\rvert_{t_0}\right)(x^j)\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\tilde{\gamma}(t_0))\left(\frac{d}{dt}\bigg\rvert_{t_0}(x^i \circ \tilde{\gamma})\right)\left(\frac{d}{dt}\bigg\rvert_{t_0}(x^j \circ \tilde{\gamma})\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))\left(\frac{d}{dt}\bigg\rvert_{t_0}(x^i \circ (\gamma \circ \varphi))\right)\left(\frac{d}{dt}\bigg\rvert_{t_0}(x^j \circ (\gamma \circ \varphi))\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))\left(\frac{d}{dt}\bigg\rvert_{t_0}(\gamma^i \circ \varphi)\right)\left(\frac{d}{dt}\bigg\rvert_{t_0}(\gamma^j \circ \varphi)\right)}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))(\dot{\gamma}^i(\varphi(t_0))\varphi'(t_0))(\dot{\gamma}^j(\varphi(t_0))\varphi'(t_0))}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))\dot{\gamma}^i(\varphi(t_0))\dot{\gamma}^j(\varphi(t_0))(\varphi'(t_0))^2}~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))\dot{\gamma}^i(\varphi(t_0))\dot{\gamma}^j(\varphi(t_0))} \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))\left(\frac{d}{dt}\bigg\rvert_{\varphi(t_0)}(x^i \circ \gamma)\right)\left(\frac{d}{dt}\bigg\rvert_{\varphi(t_0)}(x^j \circ \gamma)\right)} \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))\left(d\gamma_{\varphi(t_0)}\left(\frac{d}{dt}\bigg\rvert_{\varphi(t_0)}\right)(x^i)\right)\left(d\gamma_{\varphi(t_0)}\left(\frac{d}{dt}\bigg\rvert_{\varphi(t_0)}\right)(x^j)\right)} \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))dx^i\rvert_{\varphi(t_0)}\left(d\gamma_{\varphi(t_0)}\left(\frac{d}{dt}\bigg\rvert_{\varphi(t_0)}\right)\right)dx^j\rvert_{\varphi(t_0)}\left(d\gamma_{\varphi(t_0)}\left(\frac{d}{dt}\bigg\rvert_{\varphi(t_0)}\right)\right)} \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_c^d \sqrt{g_{ij}(\gamma(\varphi(t_0))dx^i\rvert_{\varphi(t_0)}(\gamma'(\varphi(t_0)))dx^j\rvert_{\varphi(t_0)}(\gamma'(\varphi(t_0)))} \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_c^d \sqrt{g_{\gamma(\varphi(t_0))}(\gamma'(\varphi(t_0)), \gamma'(\varphi(t_0)))} \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_c^d \lvert \gamma'(\varphi(t_0))\rvert_g \lvert \varphi'(t_0) \rvert ~dt_0 \\&= \int_a^b \lvert \gamma'(s)\rvert_g ~ds \\&= L_g(\gamma).\end{align}

The penultimate equality is due to the change of variables formula in calculus (which uses \(\lvert \varphi'(t_0) \rvert\) since \(\varphi\) is a diffeomorphism).

Arc length can also be computed on semi-Riemannian manifolds if the absolute value is used and the curve is restricted to a portion of the manifold where the metric has a consistent sign.